
Hello its a me again drifter1! Today we continue with Mathematical Analysis getting into yet another Integration Technique! The Integration of Trigonometric Functions is mostly based on Substitution, but there are also some cases where you use trigonometric equations. Trigonometric Integrals will be converted to simpler integrals that may be basic integral cases, cases that need subsitution or we may also get rational integrals. I will only tell you how to solve them directly or convert them to another known form and so checking out the other techniques is strictly important. You can check out my previous post about the Integration of Rational Functions here. So, without further do let's get started!
Trigonometric Cases we already know:
- Simple sin(x) or cos(x) integrals that are basic cases
- Product Integrals that contain a trigonometric fuction and some other function (exponential, logarithmic, polynomial) and can be solved using the Integration by Parts Technique
- Integrals that contain sinh(x) and cosh(x) that can be solved using the e^x representations of those hyperbolic functions and then Substitution of e^x with t and finally become a Rational Integral
What about integrals with more than one type of trigonometric functions or even power's of them? Well, this is exactly what we will cover in this post. Let's get into those cases one by one.
Integrals of sin^m(x)*cos^n(x) with m, n be natural numbers:
To solve such a case we have to see which one of the exponents n, m is even.
If one of the them is even than we substitute this one with t (without the exponent of course).
If both are even then we use trigonometric equations.
So, our cases are:
- m is even and n is odd than t = sin(x)
- m is odd and n is even than t = cos(x)
- m, b are both even then sin^2(x) = 1-cos(2x)/2 and cos^2(x) = 1+cos(2x)/2
- In the special case where m or n is 0 we will use the case that corresponds to even or odd exponent the same way we would use it if there wasn't a 0 there.
- If both are odd than we will create a odd/even triple-product case and then use substitution or we can also use trigonometric equations. You can do it in any way you like.
Examples:
1. One is odd

Only the exponent of sin(x) is odd and so we set t = sin(x) => dt = cos(x)dx
We will use the basic trigonometric equation cos^2(x) = 1 - sin^2(x) and so we get:
Integral(sin(x)^2*(1-sin(x)^2)cos(x)dx)
If we now replace sin(x) with t we end up with:
Integral(t^2(1-t^2)dt) = Integral(t^2dt) - Integral(t^4dt) = t^3/3 - t^5/5.
If we know set t=sin(x) we get our final result:
sin^3(x)/3 - sin^5(x)/5 + c.
2. Both are odd

Both are odd and so we replace one of them using the trigonometric equation sin^(x) + cos^(x) = 1.
So, sin^4(x)*(1-sin^2(x)) = sin^4(x) - sin^6(x)
That way we end up with two integrals that contain only one trigonometric function.
Let's use the trigonometric equation sin^2(x) = [1- cos(2x)] / 2 and replace sin^2(x) with it.
[(1-cos(2x)) /2 ]^2 - [(1-cos(2x)) /2 ]^3
The first becomes: (1 - 2cos(2x) + cos^2(2x)) /4 = 1/4 - cos(2x)/2 + cos^2(2x)/4
By setting cos^2(2x) = 1 + cos(4x) / 2 we get:
1/4 - cos(2x)/2 + (1 + cos(4x))/4
The Integral for that is: 3/8 x - 1/4 sin(2x) + 1/32 sin(4x) + c1.
The second becomes: (1 - 3cos(2x) + 3cos^2(2x) - cos^3(2x))/8
That using the same equation for cos^2(x) becomes:
1/8 - 3cos(2x)/8 + (3+cos(4x)) / 8 - cos^3(2x)/8.
For the last bit we have to solve the integral cos^3(2x) that equals:
Integral(cos(2x)(1-sin^2(2x)dx)
Setting t = sin(2x) => dt = 2cos(2x)dx we end up with:
1/2Integral(1-t^2)dt = t/2 - t^3/6 = sin(2x)/2 - sin^3(2x)/6
So, the solution for the second part is:
5x/16 - sin(2x)/4 + 3sin(4x)/64 + sin^3(2x)/48 +c2
And so our final result is:
3x/8 - sin(2x)/4 + sin(4x)/32 + 5x/16 - sin(2x)/4 + 3sin(4x)/64 + sin^3(2x)/48 +c
= x/16 - sin(4x)/64 - sin^3(2x)/48 + c.
A lot of algebra yes!
Integrals with sin(kx), cos(lx) in any "linear" combination:
To solve such integrals we will use trigonometric equations depending on the combination:
- sin(kx)cos(lx) = 1/2 (sin(kx-lx) + sin(kx+lx))
- sin(kx)sin(lx) = 1/2 (cos(kx-lx) - cos(kx+lx))
- cos(kx)cos(lx) = 1/2 (cos(kx-lx) + cos(kx+lx))
And so you form composition integrals that can be solved directly.
Examples:
1. sin(kx)cos(lx) case

Using the equation we get:
sin(3x)cos(5x) = 1/2 (sin(-2x) + sin(8x))
sin(-x) = -sin(x) as we know from simple trigonometry and so we get:
-sin(2x)/2 + sin(8x)/2
Both are simple cases and so our result is:
Integral[-sin(2x)/2 + sin(8x)/2]dx = cos(2x)/4 - cos(8x)/16 + c .
2. cos(kx)cos(lx) case
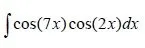
Using the equation we get:
cos(7x)cos(2x) = 1/2 (cos(5x) + cos(9x)) = cos(5x)/2 + cos(9x)/2
Both are simple cases and so our result is:
Integral[cos(5x)/2 + cos(9x)/2]dx = sin(5x)/10 + sin(9x)/18 + c .
Rational Integrals of Trigonometric Functions:
To solve rational integrals that contain sin(x) and cos(x) we again use trigonometric equations.
sin(x) = 2tan(x/2) / 1+tan^2(x/2)
cos(x) = 1 - tan^2(x/2) / 1+tan^2(x/2)
Substituting tan(x/2) with t we get the following simple equations:
sin(x) = 2t / (1+t^2) and cos(x) = (1-t^2) / (1+t^2)
So, using those last two equations you can make a rational integral of trigonometric functions into a simpler one that contains only t. Then you have to simply solve a rational integral using the technique we covered last time.
Examples:
1. sin(x) and cos(x) in denominator

We set sin(x) and cos(x) to the t equations and
t = tan(x/2) => x = 2arctan(t) => dx = 2/1+t^2 dt and so:

That finally becomes a simple 2/2-2t integral that gives us:
Integral(2/2-2t)dt = Integral(1/1-t) = - Integral(1/t-1) = -ln|t-1| + c = -ln|tan(x/2) - 1| + c
2. sin(x) and cos(x) as a quotient
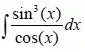
In this case we can actually do the same things as before using t = tan(x/2) or we can use a easier and faster way. I will set sin^2(x) = 1- cos^2(x) and so split sin^3(x) to sin^2(x)*sin(x). This gives us:
[(1-cos^2(x))*sin(x)] / cos(x) .
If we now set t = cos(x) => dt = -sin(x)dx we end up with:
-Integral[(1-t^2)/t dt] = -Integral(1/t)dt + Integral(t)dt = -ln|t| + t^2/2 + c
= - ln|cos(x)| + cos^2(x)/2 + c .
So, much easier than the first example!
If the integral contains other kinds of trigonometric functions like tan(x) or cot(x) etc. then we mostly first "convert" it using trigonometric equations to contain only sin(x) and cos(x) and then you get some of the known cases that we covered today or even other cases that we covered posts before. The things I covered today are more than enough to get you started tho!
And this is actually it and I hope you enjoyed it!
After all these posts about Integration techniques you are now able to solve the most types of integrals. The only thing that is left now is to solve special cases that need series and that we mostly calculate using approximation. We will get into series and sequences in some posts and also in the way that we get a approximate spolution much later on when we get into Arithmetic Methods.
Bye!
