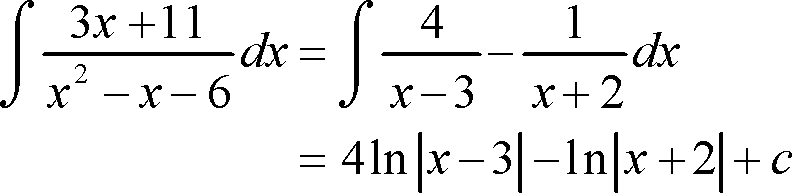
Hello its me again drifter1! Today we continue with Mathematical Analysis getting into another Integration Technique! The Integration of Rational Functions is not so difficult, but needs caution cause we can make mistakes in simple algebra calculations. You can check out my previous post about the Integration by Parts Technique here. So, without further do let's get started!
Rational Cases we already know:
Let's first get into Integrals that you already know how to solve, but are Rational.
- Integral of f'(x)/f(x) gives us ln|f(x)|+ c and doesn't need anything more
- Integral of 1/x^2+1 that gives us arctan(x) and other simple integrals like that
- Integrals of 1 / x^2 +- a^2 can be found using Substitution
- Integral of 1 / root(something) can be found using Substitution
Using Substitution to get a "solvable" rational integral:
1. If the rational function contains e^x then we set t = e^x => x = lnt and so dx = dt/t
Example:
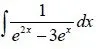
We set t = e^x and end up with:
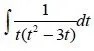
This is a rational integral that can be solved with the techniques that we will cover in a bit.
Also, don't forget that sinh(x) and cosh(x) can be represented with e^x like that:
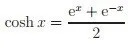
to help us solve rational integrals that contain them or even tanh(x) = sinh(x)/cosh(x).
2. If the integral contains a n-root(ax+b/cx+d), where n a natural number then we set:
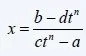and end up with a rational function that contains t and can be solved with the techniques we will cover in a sec.
If the integral contains n-roots of ax+b/cx+d with n = n1, n2, ..., nn then we find the least common multiple (LCM) of n1, n2, ..., nn and t will equal this LCM-root of ax+b/cx+d.
Rational Function Integration Techniques:
A Rational Function is a quotient of the form P(x)/Q(x) .
As you already saw previously we can use substitution to get a rational integral from difficult integrals that else would be unsolvable. But, we didn't cover how to solve this rational integral that comes out.
To solve such integral we use the so called Partial fraction decomposition or expansion method. Where we write the given quotient/fraction as a sum of other fractions with simpler denominators and numerators of a smaller degree in each fraction.
Those fractions can be:
A/(x-r)^m, where m a natural number
(Ax + B) / (x^2 + px + q)^n, where n a natural number and the equation at the denominator has no (real) solutions [p^2 - 4q <0]
Doing this we create factions that are a simple f'(x)/f(x) integrals. But, this can only be done when the degree of P(x) is smaller then the degree of Q(x). So we will try to convert quotients with degree of P(x) >= degree of Q(x) to the other form.
So, we end up with 2 cases depending on the degree.
Case 1: (degP(x) >= degQ(x))
To convert into a Case 2 quotient we have to use the polynomial division of P(x)/Q(x).
To do this we have to find a remainder r(x) and quotient q(x), with 0 <= deg r(x) <= deg Q(x) .
And then the polynomials will be connected using the equation:
P(x) = Q(x) * q(x) + r(x) => P(x)/Q(x) = q(x) + [r(x) / Q(x)]
This second one will be a integral of the second Case.
The integral of q(x) will be a pretty simple linear polynomial case.
Case 2: (degP(x) < degQ(x))
We have to follow the following steps:
1. Write Q(x) as a product of fractions of the type:
(x - r)^m, where r is the solution of Q(x)
or
(x^2 + px + q)^n, where the equation has no real solutions
2. For each fraction of the type (x-r)^m we write a sum in the form:
A1/x-r + A2/(x-r)^2 + ... + Am/(x-r)^m, where A1, A2, ..., Am are real numbers.
In the same way for each fraction of the type (x^2 + px + q)^n we write a sum in the form:
(B1x + C1) / (x^2+px+q) + (B2x + C2) / (x^2+px+q)^2 + ... + (Bnx + Cn) / (x^2+px+q)^n ,
where Bi, Ci are real numbers and i = 1, 2, ..., n
3. Every rational function can be written as a sum of fractions as we already know from simple Algebra in school and so this sum of fractions or Partial fraction expansion will be equal to the given P(x)/Q(x). So, we have to add those unlike-quantitie fractions and the denominator will be equal either way and so we will check for which Ai, Bj, Cj etc. the numerators are equal to each other. This will give us a linear system of Ai, Bj, Cj etc. that we have to solve to calculate those values.
4. The integral of P(x)/Q(x) can then be written as a sum of those fractions having Ai, Bj, Cj calculated.
Integrals of the type A / (x-r)^m are pretty simple and are a basic f'(x)/f(x) case that gives us ln|f(x)| + c.
Integrals of Ax+B / (x^2 + px + q)^n are more difficult and we have to use substitution.
Setting u = x + c such a integral will become simpler and can then be solved using the same basic f'(x)/f(x) case, other basic integrals (mostly arctanx) or even another substitution!
Examples of Rational Integrals:
1. (x-r)^m example
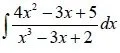
Because degP(x) < deg Q(x) we are in Case2 directly and can start following the steps.
x^3 - 3x + 2 = (x - 1)^2*(x + 2)
So, (x - 1) ^2 will become two factions A/x-1 + B/(x-1)^2
(x + 2) will get only one faction C/x+2
This means that P(x)/Q(x) = A/x-1 + B/(x-1)^2 + C/x+2 that becomes:
P(x) / Q(x) = A(x-1)(x+2) + B(x+2) + C(x-1)^2 / (x+2)(x-1)^2
Where the numerator is equal to: (A+C)x^2 + (A+B-2C)x + (-2A+2B+C)
We want P(x) to be equal to the numerator and so we have to solve the linear system:
4x^2= (A+C)x^2 => 4 = A + C
-3x = (A+B-2C)x => -3 = A + B - 2C
5 = -2A + 2B + C
Solving this system with any method you like you will end up with:
A = 1, B = 2 and C = 3
And so P(x)/Q(x) = 1/x-1 + 2/(x-1)^2 + 3/x+2.
Integral(P(x)/Q(x))dx = integral(1/x-1)dx + 2*integral(1/(x-1)^2)dx + 3*integral(1/x+2)dx
= ln|x-1| + 2*(-1)*1/(x-1) + 3*ln|x+2| +c = ln|x-1| -2/x-1 + 3*ln|x+2| + c
2. (x^2 + px + q)^n example
Because degP(x) < deg Q(x) we are again in Case2.
x^2 + 2 = 0 has no solutions and so we have to write P(x)/Q(x) as a sum of fractions like that:
(Ax + B) / (x^2+2) + (Cx + D) / (x^2+2)^2
If we add those fractions we end up with:
P(x)/Q(x) = Ax^3 + Bx^2 + (2A+C)x + (2B+D) / (x^2+2)^2
We want P(x) = x^3 = Ax^3 + Bx^2 + (2A+C)x + (2B+D) and so:
x^3 = Ax^3 => A = 1
0x^2 = Bx^2 => B = 0
0x = (2A+C)x => -2A = C => C = -2
0 = 2B + D => D = -2B => D = 0
So, A = 1, B = D = 0 and C = -2.
Setting those values on our fraction sum we end up with:
P(x)/Q(x) = x/(x^2+2) + -2x/(x^2+2)^2.
Integral(P(x)/Q(x))dx = integral(x/(x^2+2))dx + integral(-2x/(x^2+2)^2)dx
The first one is again a ln|f(x)| case and the second again a power case and so the result is:
1/2*ln(x^2+2) + 1/(x^2+2) + c
3. combined types of fractions
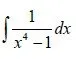
You can directly see that P(x) < Q(x).
x^4 - 1 = (x-1)(x+1)(x^2 + 1)
So, we have two types of fractions and 1/x^4-1 now looks like this:
A/x-1 + B/x+1 + Cx+D/(x^2+1) = (A+B+C)x^3 + (A-B+D)x^2 + (A+B-C)x + (A-B-D) / x^4-1
If we set 1 equal to the numerator we end up with the following system:
A+B+C = 0
A-B+D = 0
A+B-C = 0
A-B-D = 1
If you solve this system using any method you like you will end up with:
A = 1/4, B = -1/4, C = 0, D = -1/2
And so our integral now looks like this:
integral(P(x)/Q(x))dx = 1/4*integral(1/x-1)dx -1/4*integral(1/x+1)dx -1/2*integral(1/x^2+1).
The first two are simple ln|f(x)| cases, but the last one is interesting cause its actually arctan(x)!
So, our final result is: 1/4*ln|x-1| -1/4*ln|x+1| - 1/2*arctan(x) + c
4. In Case1
degP(x)>degQ(x) and so we are in Case1
Knowing how to divide polynomials you do the following:
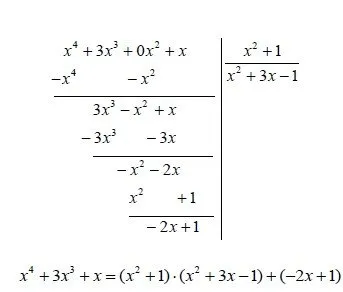
This explains them pretty good if you don't know them already.
This means that we know have to solve the integral:
x^2+3x -1 + (-2x+1)/x^2+1
We know that x^2+1 has no solution and so we can't tranform it into a Case 2. This means that we will try to create simple integrals in another way. We will simply rewrite the numerator as -2x +1 = -(x^2+1)' + 1 and solve the simple ln|f(x)| case and create a simple arctan(x) case.
So, our final integral is:
Integral(P(x)/Q(x)) = integral(x^2+3x-1)dx - integral(x^2+1)'/(x^2+1))dx + integral(1/x^2+1)dx
= x^3/3 + 3x^2/2 - x - ln(x^2+1) + arctan(x) + c .
Try solving the e^x integral example that we didn't finished with the function that contains t.
You must get ln|t^2 - 25| + c = ln|e^(2x) - 25| + c
And this is actually today's post and I hope you enjoyed it!
The next and final techniques that I will cover in our series will be about solving integrals of trigonometric functions. After that we will get into how we solve Limits that contain Roots, something that I completely forgot to talk about my Limit posts.
Bye!