Chaos Theory
What a seemingly strange name for a discipline! What is this chaos to which mathematicians and scientists make allusions? Maybe they're living in a grand illusion? And, no, I am not speaking of the holographic universe model nor especially one with Charon ferrying people across a river.
Let me first make a very important note. Mathematics and science in general that is publicly funded is all about story-telling and even more about marketing (although, one could argue that there is a lack of good marketing for mathematics).
As the story unfolds, observers see the playfulness that comes with the territory. Often, sexual innuendos dot the landscape. If you do not think that certain concepts and phrases--the pigeon hole principle, groups, group actions, the center of a group action, dirty data, cleaning dirty data, etc.--are innuendos, then I dunno what to tell you. Maybe it's me that thinks certain terms used in mathematics and science are made to sound sexual. I have no idea since no one comes right out and says anything along this line of thought, mainly due to societal norms and political correctness. However, the metaphor is always in the back of my mind.
Anyway, let us return to ChA0s ...
History of Chaos Theory
Chaos was originally termed by T. Y. Li and James A. Yorke in their seminal paper Period 3 Implies Chaos and was originally observed by Lorenz when conducting weather simulations. Lorenz found that if he used slightly different parameters (but relatively close!) for the input of his simulations, the results of the simulation would range wildly, seemingly in a (deterministically known) chaotic fashion. This observation became known as Sensitivity to Initial Conditions.
Chaos as Mixing
Chaos, in a nutshell, can be seen as a type of 'mixing theory.' Since 'chaos' sounds more sexy than 'mixing' (although, mixing can be a little sexy -- my mind goes back to college mixers), and probably since it was the original term, the field is Chaos Theory as opposed to Mixing Theory. The nomenclature probably also comes from looking at fractals at odd hours of the day and staring at the seemingly random and chaotic patterns that emerge from following simple rules. These visualizations provide an alternative (beyond algebra and analysis) to study Chaos Theory.
The Mandelbrot Set

The 'Sea-horse' Valley
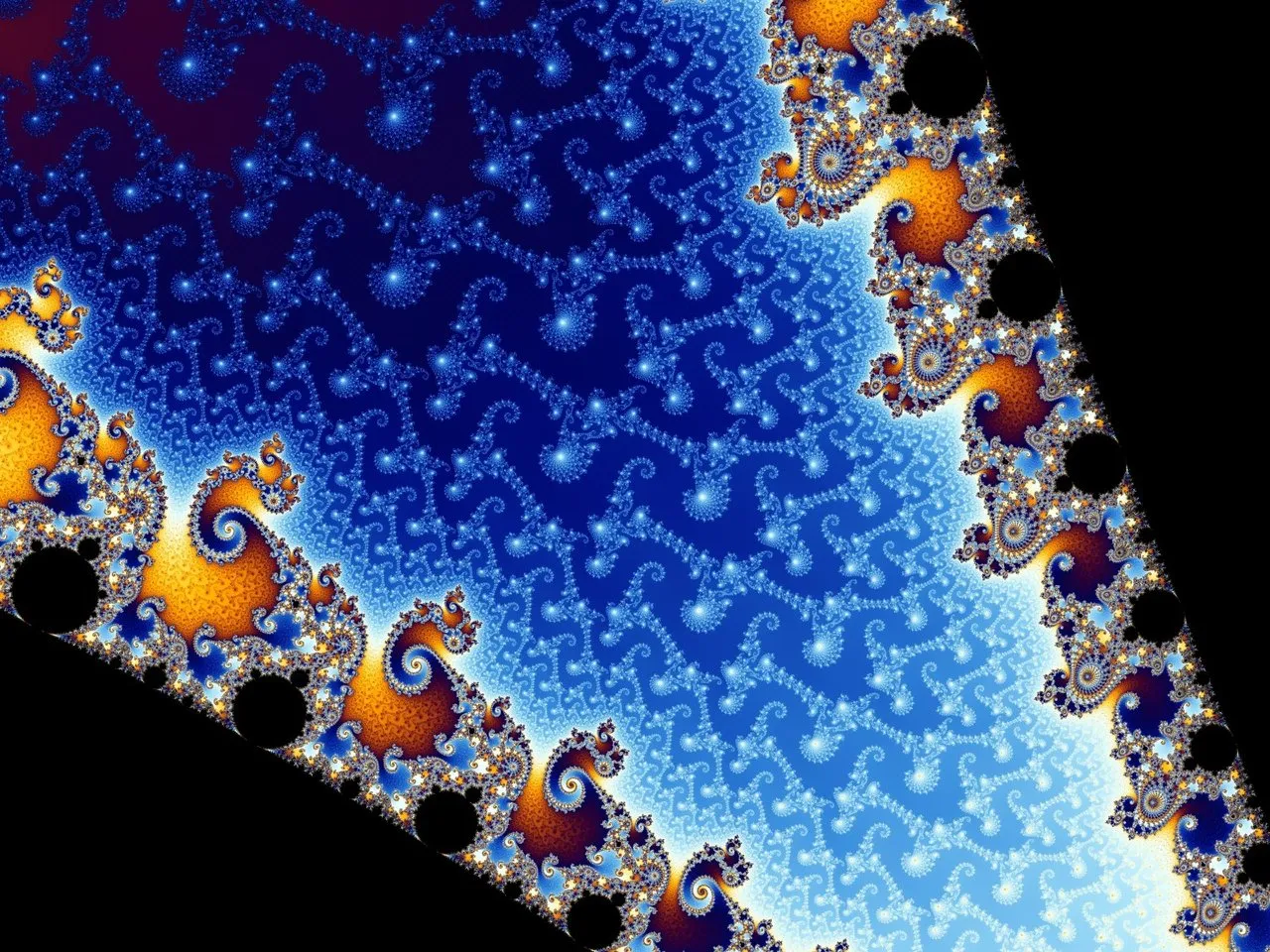
I had a mathematics professor during my undergraduate years who described Chaos Theory as mixing theory to me. At the time, we were researching Symbolic Dynamics and considering a generalization of the Tent Map to a map with N piecewise linear functions with the same slope on the unit interval.
Q: What is being mixed?
A: Points in a space.
One considers a function F that takes as input a point in domain (or space) and spits out as a result a different point that same domain. Mathematically, we write F : D -> D.
In Symbolic Dynamics, you subdivide your domain into finite pieces and label them, say from
X_1, X_2, ..., X_n.
With the unit interval, i.e. D = [0,1], you can let X_1 = [0, 1/n), X_2 = [1/n, 2/n), ..., X_i = [(i-1)/n, i/n), ..., X_n = [(n-1)/n, 1]. One then wants to study the differences in the itinerary of two points, x and y, in the space. An itinerary is constructed by re-using the output as a new input using the function F.
Often, we want to consider neighboring points, or points that within some specified distance from one another. This information tells us how the space becomes 'mixed' over time (if it even does!) as you iterate over the same function. The basic notion is that if two points are close to one another initially, then eventually over time (which means more iterations), the itineraries will be vastly different.
What happens in chaotic systems is that the itineraries of two points match closely for awhile, the points separate and move apart, and then over more iterations of the function, will come back together. This pattern is repeated over and over again in 'chaotic systems.'
Let us consider a simple example.
Let us look at the Tent Map (named, because it looks like a simple tent) on the unit interval. This function is
F : [0,1] -> [0,1] with the rule for F being
F(x) = 2x, if x < 1/2
F(x) = -2x + 2 if x >= 1/2.
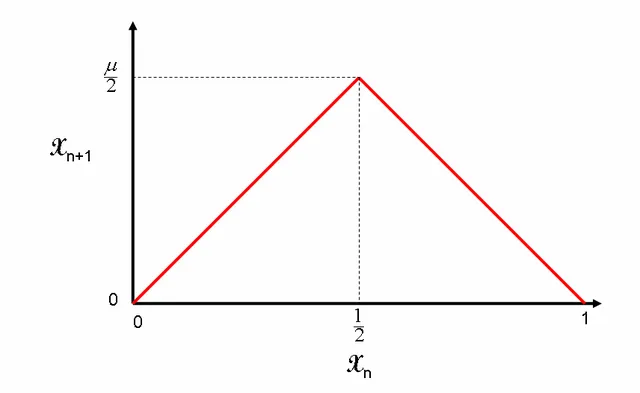
Let's label the two intervals [0,1/2) = A and [1/2,1] = B
Now, we want to consider the itineraries of x =(.5)^.5 and y=0.7071 in terms of A and B. These two points are close in their initial conditions, but by comparing the symbolic itinerary, we will observe that the itineraries diverge, converge, diverge, etc., in a (deterministic) chaotic fashion.
We write F^{k}(x) to indicate the k'th iteration of the function F on a point x. Let's compare the first 30 'stops' in the itineraries for x and y, in terms of their location on the map.
We compute quickly that the chosen 'x' and 'y' have 17 iterations in common (including the initial starting location), and we see that as soon as divergence occurs (which will happen if the points are unique), that when the itineraries converge is (deterministically) random.
Here are the two itineraries :
Itinerary(x) = BBBABBBBBAAAABBABAAABABABAB
Itinerary(y) = BBBABBBBBAAAABBABBAAAAABBBA
Now, one can partition a domain in a multitude of ways, 2-way partitions, 3-way partitions, .., k-way partitions and play this same game again and compare the itineraries of different points.
Fixed points
A fundamental object of study in Chaos Theory is the notion of a 'fixed point in space'. This means that given a function F on a domain D, what are all the points in the space that always gives the same output as input, i.e. F(x) = x.
When viewed from the Symbolic Dynamics world, this is saying that from all iterations onward, the location of a point is in the same labeled portion of the space.
Formally, we would say that there exists a finite k such that for all l > k, F^{l} = X_i.
The two fixed points of the tent map are thus x = 0 and x = 2/3.
Period-k points
We can extend the notion of fixed points of a map and the (uninteresting) Symbolic Dynamics that comes with these fixed points to periodicity k points. Mathematically, we are then solving for points that satisfy
F^{k}(x) = x.
If we move over to the Symbolic Dynamics world, then a point x has periodicity k if its itinerary repeats itself at every k'th step.
Conclusion
So, Li and Yorke's main result says that if you have an iterative function and if you can find a point that has periodicity 3, then (mathematical) chaos ensues. It doesn't matter what the function is, as long as there exists a 3-periodic point!
The Aftermath
One can start delving into stranger territories like 'invariant spaces', mixing with respect to fluids as they flow over time (a question to ask does one expect complete mixing of a fluid or not?), Mandelbrot sets and their corresponding Julia Sets, visualizations of other functions iterations over time, Newton basins of attraction, properties of the itineraries of irrational and rational points, etc.
Newton Basins of Attraction

Some Julia Sets


Cool fact
Instead of the tent map, consider the map:
F(x) = 2*x, if x < 1/2
F(x) = 2*x - 1, if x >= 1/2
Instead of labeling the locations of the points as A or B, we will use 0 or 1, with the same convention as before. It turns out that the itinerary of a point is the same as its binary expansion! Crazy, huh?!
What's even cooler is that one can generalize the binary expansion to any finite number of k symbols and find any point's k-ary expansion by constructing the right function.
Exercise : What's this function look like?