Hello! It's me again and today we start out with something new. We will talk about Logic Design now for a lot of posts. I will start with Theory, continue on with Implemenation using MultiSim, talk about some advanced Theory stuff and then get into VHDL and maybe even Verilog that let us write Logical Circuits in Code. Today, we start with Numeral Systems. I will talk about the represenation of some Systems, some basic operations (add, sub, mul and div) and conversions from and to those Systems. So, without further do. Let's get started!

Decimal System:

We all are familiar with the decimal numeral system that we use everyday. This system uses 10 digits with characters being " 0, 1, 2, 3, 4, 5, 6, 7, 8, 9" and we can write any number we want using those 10 digits. We all can do stuff like adding, subtracting, multipling, dividing numbers that are represented in decimal system, cause this is the system we learned to use in school when we were young.

But, this is not the only system in which we can represent numbers. How can a computer know which number it should operate when it only can take 2 volt values (low and high or 0 and 1). We could split the volt region into 10 parts to make it understand 10 different numbers as we are used to do in real life calculations, but it would have a big cost to create those and the logical chips/circuits would also be to complicated. That's why we use another System for operations inside of a computer.

Another way of representation:

An decimal number can also be represented using power's of 10 like this:

digit * 10^3 + digit * 10^2 + digit * 10^1 + digit* 10^ 0 = number

In the same way we can do this in any System like this:

digit * system_digits ^ N + digit * system_digits ^ N-1 + ... + digit * system_digits ^ 0 = number

Binary System:

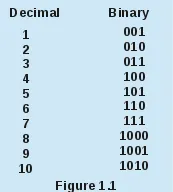
The binary numeral system uses 2 digits that are 0 (low) and 1 (high) that represented low voltage and high voltage as input to a logical gate or circuit. Using 0's and 1's the computer does calculations, having each number contain 0's and 1's. So, an number in binary system could look like this: 01011011. We mostly use 8 Bits cause they can be stored inside of 1 Byte that is the smallest storage unit (in generall) of an computer. To differentiate a number from one to another system we use an smaller 2, 8, 10, 16 and so on, at the bottom right of a given number, to know in which system this number is given (I can't do it here that easily, so I will always say what kind of numbers we use).

Using 0's and 1's a computer can then do all kinds of operations and the operation system knows which binary number stands for which ASCII Character or Unicode Character and that's how we then from Characters and Words printed into the Screen using only 0 and 1 sequences.

Adding Binary Numbers:

To add 2 or more binary numbers we start from the right the same way we used to do it when adding in decimal system. When both numbers are 0 we don't do anything, when one is 1 and the other 0 then the result is 1 and when both are 1 we have a carry that we pass over to the left. So, when we have two 1's and a carry (1) we put 1 as result and then pass the carry over to the left again and so on...

Example:

00110101

+ 10100011

--------------

(1)0

(1)00

(1)000

1000

11000

(1)011000

1011000

= 11011000

Subtracting Binary Numbers:

To subtract binary numbers we add! Yeah you heard it right. We have to convert our binary number to its 2' complement inverting all the digits from 0 to 1 and afterwards adding 1 to it. We then do normal addition using those two numbers, but the result will contain 1 digit more that we will discard.

For example when we have 01011010 and want to get it's 2's complement we do the following:

invert digits: 10100101
add 1 to it: 10100101 + 1 = 10100110

Example:

10100110 - 00101001 = ?

2's complement of 00101001 = 11010110 + 1 = 11010111

So, we do 10100110 + 11010111 = ?

10100110 + 11010111 = 101111101 (and we discard the first digit so we get) = 01111101

Multiplying Binary Numbers:

To multiply binary numbers we use the same concept we used in decimal. We will add the value's, shifting the numbers to the left each time and using one digit at the time (from one of the two numbers).

Example:

101

x 011

--------

101 (1* 101)

1010 (1 * 101, shifted one to the left)

00000 (0 * 101, shifted two to the left)

+ (011 is the second number)

--------

= 1111

Diving Binary Numbers:

To divide 2 binary numbers we do the same we did in decimal. We will use the Euclidean division that gives us quotient and remainder.

Example:

We check if our divident can be divided by our divider. We will take the digits of our divider down one by one until the divident can't be put inside anymore. The the division can be done we will write 1 in the result, else 0. And the end result is our quotient and what remains down is our remainder.

101/111011 = 1011 (quotient)

111

-101

-----

1001

- 101

------

1001

- 101

--------

100 (remainder)

We could continue on to find a result with floating point number. So, after reaching the point where our divident can't fit inside of our dividor we add 0's to our remainder and the quotient get's a floating point symbol (.) and we continue on like this:

101/111011 = 1011.11 (quotient only, no remainder)

111

-101

-----

1001

- 101

------

1001

- 101

--------

1000

- 101

--------

110

- 101

------

1 (1 as remainder means we are finished)

Converting from Decimal to Binary:

All that Operations are pretty nice, but how do we get a binary representation of an decimal number. It's pretty easy. We simply have to divide our number by 2 until the number we divide with is 1 and afterwards we read the results (0 or 1) we got in between in opposite order ( we did that in an assembly code already :D ).

Example:

12 in decimal is ? in binary

12/2 = 6 (0)

6/2 = 3 (0)

3/2 = 1 (1)

1/1 = 1 (1)

(here we write the remainder)

So, our number is 1100 (we read the remainder in opposite order)

Converting from Binary to Decimal:

To convert from binary to decimal the process is even easier. We know that each digit in a number system represents an power of the system. In binary the power will be a power of 2. So, the top right number is the power of 2^0 that equals 1, that power of the second one is 2^1 = 2 and so on...

So, an binary number can be representated in decimal like this:

1 * 2^3 + 1 * 2^2 + 0 * 2^1 + 1 * 2^0 = 11o1 (binary)

Example:

So, the number I listed above (1101) from binary to decimal can be converted like this:

1101 = 1 * 2^3 + 1 * 2^2 + 0 * 2^1 + 1 * 2^0 = 8 + 4 + 0 + 1 = 13

Other Numeral Systems:

Systems that are commonly used are the Octal and Hexadecimal systems. The Octal uses 8 Digits and the Hexadecimal uses 16, that are more then the Decimal ones.

Octal System:

The Octal system uses the digits "0, 1, 2, 3, 4, 5, 6, 7" and we can do all the operations we know again. But, we should not be confused by the Decimal, cause now we don't use 10's but 8's to calculate.

Example Operation:

Suppose we want to calculate how much 35 + 25 gives us.

35 + 25 is not 60, cause we are in octal so, we have to do the calculations one by one, checking carry's like that:

+ 25

-------

(1)2

Yeah, the result is 62, cause we had a carry of 1 when we surpassed 8!

The other operations work in the same way.

Converting from Binary to Octal:

it's pretty easy to convert from binary to octal, cause we take the numbers in pairs of 3 from the right to the left and write the octal/decimal number these 3 binary's represent (3 digits of binary can be at most 111 that is 7)

Example:

10010110 (binary) = x (octal)

010010110

--- --- ---

010 010 110

2 2 6

So, the number in octal is 226

Hexadecimal System:

The hexadecimal system uses some new digits, cause the ones from our decimal system are not enough. So, the digits of this system are: "0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F". We again should be careful when dealing with those numbers, cause the result will not be the same as in decimal calculations.

The less digits we have, the larger the number gets and the more digits we have, the smaller the number gets!

Example Operations:

Suppose we want to calculate again how much 25+35 gives us.

It again doesn't give us 60 as we are used to do in decimal.

+ 35

------

= 5A ( yeah I know those letters are confusing, but A = 10! )

Let's do one more with bigger numbers that contain letters.

6A4 + 3C5 = ?

6A4

+ 3C5

-------

9 ( no problem at all)

(1)69 ( A + C = 10 + 12 = 22 and 22 - 16 = 6, so we have a result of 6 and a remainder)

= A69 (6 + 3 + 1 = 10 that is represented as A in hexadecimal)

Converting from Binary to Hexadecimal:

We will again use the same trick we used in Octal, but this time we will get the numbers in pairs of 4.

So, 100101101011 (binary) = x (hexadecimal)

---- ---- ----

1001 0110 1011

9 6 B

Our number is 96B in hexadecimal.

I will not use those last two that much, but I wanted to point out some things only, for you to understand them more! The most stuff we will do has to do with the binary system that computers use!

This was all that I wanted to show you today! Hope you enjoyed it and learned something new.

Next time we will talk about Logical (Boolean) Functions. And just for you to know, I'm thinking of posting some Code Posts in between of those Theoretical Posts of Logic Design, because I have enough posts to make and some viewers may not be interested in those things, so I will try to upload some other stuff also sometimes! :)

Bye!

Logic Design - Numeral Systems

Decimal System:

Another way of representation:

Binary System:

Adding Binary Numbers:

Subtracting Binary Numbers:

Multiplying Binary Numbers:

Diving Binary Numbers:

Converting from Decimal to Binary:

Converting from Binary to Decimal:

Other Numeral Systems:

Octal System:

Hexadecimal System: