Hello its'a me again! Today I will talk about Boolean Algebra and Simplification Theorems that will help us simplify our boolean logic circuit function (that we talked about last time). So, without further do! Let's get straight into it!
Quick Reminders:
As we already know from last time, a circuit is represented by a function. Those combinational logic circuits use 2 or more basic logic gates to implement more advanced circuit functions. But, an circuit can be represented by more than 1 function and so we have to find the simplest one.
Last time I showed you a way of getting a circuit function using the minterms or maxterms of an circuit's truth table. But, this function was either to big or even when it was small it would contain to complicated elements that translate into complicated circuits.
Boolean Algebra:
To make our function simpler and so our circuit, we use Boolean Simplification Theorems. Boole was an mathematician that wrote the Boolean Algebra theory that let's us simplify a circuit's function.
The basic operations that are needed to make any circuit are: "NOT, OR, AND", and using those we create other more advanced circuits (I will talk about the basic logic gates some posts later on). OR is represented by an '+'(addition or disjuction), AND by nothing or an "*"(multiplication or conjuction) and NOT gives us the opposite input (0 -> 1, 1 -> 0) and is mostly represented by an '(negation).
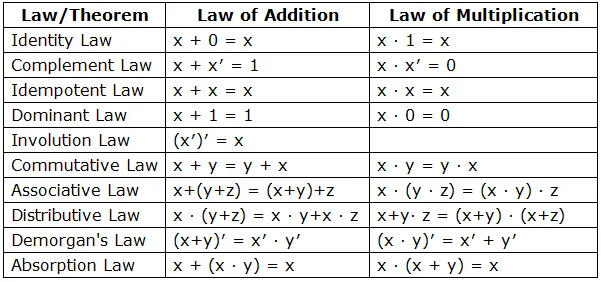
So, the Boolean Algebra contains Laws and Rules that let us modify our function, without changing the output, so that we end up with an simpler function for the same input/output values (remember 1 truth table gives us many function).
Laws from Ordinary Algebra:
Boolean Algebra uses 2 values, 0 (false) and 1 (true). So, it represents exactly the way an computer talks. We will use the binary representation to keep it simpler. There are some Laws that the Boolean Algebra takes from the Ordinary Algebra.
Those are:
- Commutativity of Addition (A + B = B + A) and Multiplication (AB = BA)
- Associativity of Addition [A + (B + C) = (A+B) + C ] and Multiplication (A(BC) = (AB)C)
- Distributivity of Multiplication over Addition [A(B + C) = AB + AC) or (A + B)(C + D) = AC + AD + BC + BD]
Simple Rules of 0 and 1 (best name for them I guess):
- Annihilator of Multiplication: Anything that multiplies (AND) with 0 gives 0 (A * 0 = 0)
- Annihilator of Addition: Anything that adds (OR) with 1 gives 1 (A + 1 = 1)
- Identity for Multiplication: Anything that multiplies (AND) with 1 gives itself (A * 1 = A)
- Identity for Addition: Anything that adds (OR) with 0 gives itself (A + 0 = A)
All except the second one hold in Ordinary and Boolean Algebra.
Boolean Algebra only Laws:
- Idempotence: Add or Multiply with self gives self (AA = A and A + A = A)
- Absorption: Special Case of Distributivity [A(A + B) = A and A + AB = A]
- Distributivity of Addition over Multiplication [A + BC = AB + AC]
Complement Laws:
- Anything multiplied(AND) with its complement gives 0 (A*A' = 0)
- Anything added(AND) with its complement gives 1(A + A' = 1)
- If we complement two times we get ourself again (A'' = A)
- Using the Truth Table we know that A + A'B = A + B and A' + AB = A' + B. So, when having both the "one" that is alone survives and the "one" that is together with another variable gets cleared!
De Morgan Theorem:
The De Morgan Theorem is used to make our Circuit even smaller including more gates then the AND, OR, NOT Gates. Using the Universal NOR and NAND Gates we can then simplify our Circuit even further (We will talk about them separatelly some posts later on)
The Theorem for two variables looks like this:
- (AB)' = A' + B'
- (A + B)' = A'B'
A simple way of memorizing it is that AND turns into OR and vise versa, and A turns into NOT A or A' and vise versa.
So, we can generalize it for even more:
- (ABC)' = A' + B' + C'
- (A + B + C)' = A'B'C'
Using this Theorem we can get rid of all the Complements putting them all together and making them into an NAND or NOR Gate [NAND is actually (AB)' and NOR is actually (A+B)'].
Example Simplification:
Suppose we have a circuit and we want to simplify it. The circuit function of that logical circuit contains only basic Gates (AND, OR, NOT) and we want to keep using only those basic Gates.
The function looks like this:
F(A, B, C) = (A+B)B' + B' + BC
We use the Distributivity Law [(A+B)B' = AB' + BB']:
F(A, B, C) = AB' + BB' + B' + BC
We use one of the Complement Law(BB' = 0) and afterwards the Identity of Addition (AB' + 0 = AB'):
F(A, B, C) = AB' + B' + BC
We take a common factor B' of the first two:
F(A, B, C) = B'(A + 1) + BC
We use the Annihilator of Addition (A + 1 = 1) and afterwards the Identity of Multiplication (B '* 1 = B'):
F(A, B, C) = B' + BC
We use the Complement Law (B' + BC = B' + C):
F(A, B, C) = B' + C
The last expression is the simplified function. As you can see we don't have A as an input anymore cause it is not needed for getting the specific output values that this circuit gave us!
So, our Circuit now contains only two Gates: An OR Gate that connects the two Inputs and an NOT Gate that inverts the B Input's value!
This is the end of today's post. Hope you learned something new and enjoyed it!
You should always open this or your notes from all that stuff when simplifying, cause the smallest mistake could cause your new function to not representate the same Truth Table anymore!
Next time we will get into Karnaugh Map Simplifaction that is much easier than all that mathematical calculation stuff that I showed you today, but sometimes even Karnaugh Map could give us a result that we don't like, and knowing the Theorems that apply to an Boolean Function we can then tweak it a little to make it even better!
Until next time..Bye!
