
Hello my friends! From today we start getting into more advanced Circuits that are implemented using the Basic and Universal Gates we talked about the last 3 posts! Today's post is all about Adder Circuits, with whom we can make binary additions! We will start out with Half-Adders, continue on with Full-Adders and lastly talk about N-Bit Adders that use 1 Half-Adder and as many Full-Adders as you wish! I will also make a little introduction into Subbers, that are pretty easy to make if we know N-Bit Adders. So, let's get straight into it!
Binary Addition:
As you already know in Circuits we use the Binary System, cause we can have low(0) and high(1) voltage that can be translated easily into 0 and 1 binary numbers to make our life easier. When adding two 1-bit numbers that result can be 0, 1 or 10, so will have an Output Bit-length of 2. When adding three 1-bit numbers that result can be 0, 1, 10 or 11, so we again have an Output bit-length of 2. This exact concept will be used in all of the Adder Circuits we will talk about today!
Half Adders:
Let's start out with Half Adders. An Half Adder is a Circuit that gets 2 Inputs and gives back 2 Outputs. The Inputs are 2 1-bit numbers that we want to add. The Outputs are the Sum and the Carry, cause like I said earlier we can have at mostly an 2-bit Output (0, 1, 10). The Sum is then a part of our result and the Carry either is a part of the result (if it was our last Gate) or it will be passed as Carry Input to the next Adder that will be a Full-Adder!
So, looking into the Logic it must perform the Truth Table makes sense to be like that:

It is a little bit strange to see Carry and Sum in switched places if we think about 1 + 1 = 10 and see an 01 at the last 2 columns. But, it also makes sense!
Using this Truth Table we can create an Logical Circuit pretty easily! We will find a boolean function for the outputs sum and carry and then translate it into an Gate or Combination of Gates (that this time is not needed as you see in a bit).
Sum:
Taking the minterms we end up with the function Sum = A'B + AB' that translate into an XOR Gate A⊕B, as we said last time! So, our Sum part will be a XOR Gate!
Carry:
The Carry one is pretty easy. We see that there is a Output of 1 only when both Inputs are 1, so we have an AND Gate!
So, our Circuit looks like this:

where S = A⊕B and C = AB
Full-Adders:
Full-Adders work almost the same! The only change is that we now have three 1-bit inputs and an 2-bit Output! The Inputs are the two 1-bit numbers to add and the carry in from the previous Adder that may be an Half or Full-Adder! The Output is again a Sum and Carry out!
When adding three 1-bit numbers the result is again at most 2-bit long, but we now have a larger Truth Table that looks like this:

Using this Truth Table we can then make our Logical Circuit! We will have 2 Outputs that are Sum and Carry out and so will have to find out 2 Logical Functions that then will be made into a Circuit!
Sum:
Sum is pretty easy if you remember what I told you last time! As you can see we have an Output of 1 in Sum only when the number of 1's in the Input is odd. That means that we have an XOR-3 Gate and so our Sum Function is Sum = A⊕B⊕C. But we will implement it as Sum = (A⊕B)⊕C to minimize the Gate usage in general!
Carry Out:
If we take the Minterms of the Truth Table we end up with: Carry Out = A'BC + AB'C + ABC' + ABC. It looks pretty similar to the XNOR Gate I talked about last time, but ABC is actually A'B'C' in that representation if you check it out! We will simplify it using Boolean Algebra tho. If we take C as common factor in the first two terms we end up with C(A'B + AB') that is C(A⊕B). In the last two terms only C changes (similar to how we form groups in Karnaugh Map) and so we can put those two together as AB.
So, our final Function is: Carry Out = AB + C(A⊕B) and the Circuit looks like this:

where S = (A⊕B)⊕Cin and Cout = AB + Cin(A⊕B).
N-Bit Adders:
When Adding Numbers with more than 1-bits we will have to use the so called N-Bit Adders! A N-Bit Adder is made by joining an Half-Adder and N-1 Full-Adders (you can also use N Full-Adders, but the first one will not have a Carry in!). The Carry out of the first Adder will be passed as an Carry in of the next Gate and the final Carry out will be part of our result. We will start out adding the Bits starting from right and going to the left, cause that's how the Carry is made (remember how we did 8-Bit Binary Addition when we talked about Numeral Systems).
So, an N-Bit Adder Circuit looks like this:
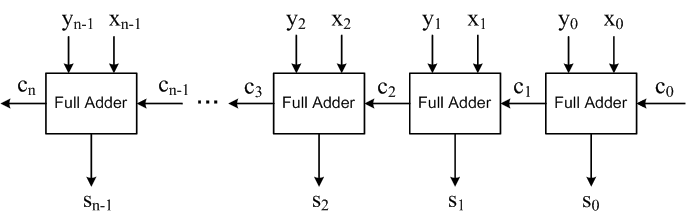
where you can change the first Full-Adder in the Chain with an Half-Adder if you like!
N-Bit Subber:
Using the N-Bit Adder concept and tweaking the Inputs a little we successfully create an N-bit Subber Circuit! We simply have put the second 1-bit number that gets added into an XOR Gate with the other value being 1 directly. We also have to put an XOR Gate in the final Carry together with an value of 1 again.
So, the Circuit looks like this:

This is the end of today's post! Hope you enjoyed it!
Next time in Logic Design we will get into more complex Circuits that are the Multiplexers, Encoders and Decoders!
Until next time...
