Hello math bugs(🐞) and hivers(🐝)
I hope you are strong & sout and doing good in life.
As you have seen ,my post today is about finding maximum and minimum value of algebraic expression.First I'll start with basic concepts and then will go to deeper.
We want to find max or min value of a expression where we find variable(x,y,z etc).While finding it we have to put value of the given variable for that the entire value of the expression can be found in terms of minimum and maximum of it.
Let's take a simple algebraic expression. Say (x²+5). If we want find min value of the expression we put Zero in place of x. So the minimum value of (x²+5) is 5 at x=0. Let's check other +ve or -ve values of x what gives us. If we put any positive integers , the value of expression will be more than 5 and if we put any -ve value x it will produce also positive as there is x² because square will make it +ve and thus in this case the value of the expression will also be more than **5.If we want to find max value , increase or decrease the value of x and it will lead you to infinite ♾️ and max value will be infinite.let's check it below:
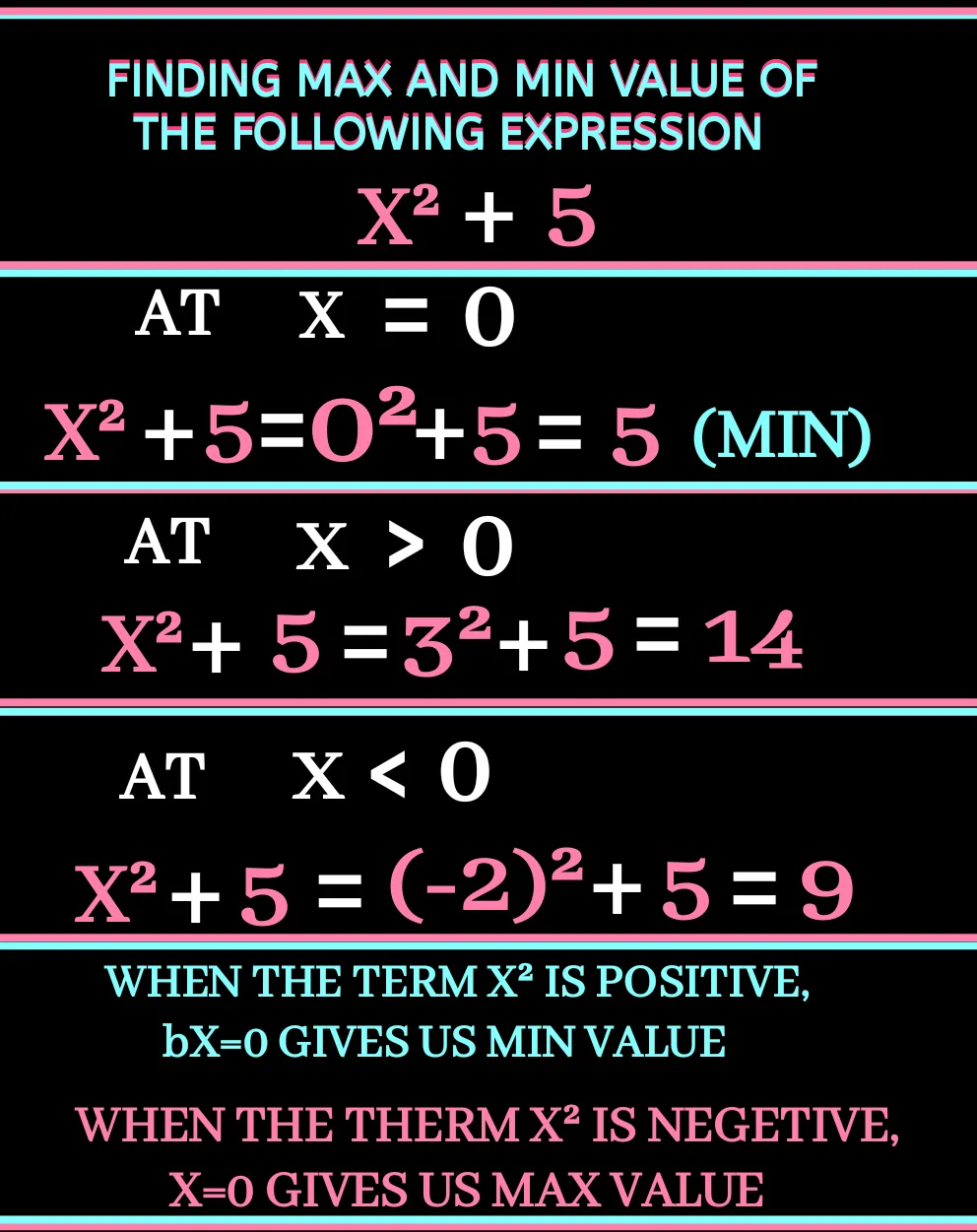
Let's take another example. Say (-x²+5).I this case min value will be 5 and max value will be infinite ♾️. If we put Zero in place of x the value becomes 5 but any other +ve or -ve value of x, will make it a higher valued expression let say x=10. It bring value of the expression 105 and which is greater than 5. If we put -10, it will bring the same value as x² will make it positive. Let's check details
In the following picture:

Note:
1️⃣ To determine max or min value of an algebraic expression we have make a perfect square and the part wich is not included in doing so, will be min or max value.
2️⃣ When term x² is positive, it will give min value at x=0 and when the term x² is negetive, it will give us max value at x=0.
I hope you have got the basic idea of max and min value of an algebraic expression and how to find its min and Max values.Now it's time to use this concept in a little advance algebraic expression.
Let's take (x²+7x+8). Now again we are going to find out max and minimum value of the expression.Here we have two terms having the variable x. So only making the term x² equals to zero, won't able us to find max and min values. We gonna take both x² and x inside perfect square. let's check details:

Note:
1️⃣ If the given expression is like (x² + bx + c),
put x= -b/2 to get minimum value.
2️⃣ If the given expression is like (-x² +bx + c),
put x= b/2 to get maximum value.
3️⃣ If the given expression is like (ax² + bx +c), first get rid of number coefficient of x². That means take that 'a' common. Check it below:

Important note: We can't find maximum and minimum value at the same time. If we can find minimum value of an algebraic expression, the maximum value will be infinite(♾️) and vice versa.
Till now we have seen algebraic process but we have better way to handle the problem.Now we gonna use calculas to get the maximum and minimum values of quadratic and cubic or any other degree of algebraic expression.
Now you need to have knowledge about derivatives (dy/dx).I won't explain it in details 😅😅.But I will show how to apply it and in that case I will use the last problem where the expression was (4x²+5x+6).
Let's find the minimum value of it with calculas (Derivatives).First we have to find the derivates of the expression and then to put the derivates equals to zero to find the value of x what will give us max or min values. If derivate is negetive, we can find max value and if the derivate is positive we can find least or minimum value of the expression. Here in the expression (4x²+5x+6) derivates will be positive and so value of x will be negetive and we easily can find minimum value of it.
let's check it below:

In previous photo I have shown you how we can have the required value . So check it there.
If you have any problem to have a complete knowledge about mxima and mimima of algebraic expression , please feel free to write a comment below the post. I'll happy to help and your response to my post will be appreciated.
If you find any mistake , pleas let me know as I may overlook something😭 to draw all the drawing.Sorry for that.lol it's hilarious to draw the drawing to post a math problem. Though takes me a lot of time to do so.
Someone commented on my previous post . I appreciate his comment. He said I should share the source of my post for that people can get more information about the topic and for verifying what I am saying. First of all I don't use any reference what I share is my knowledge I gathered in school, colleages and teaching knowledge. I tried to find in the internet if I could share link of more detailing but I was in vain. My search will continue and I hope I can include link soon when I got good source.
I hope you have liked my post today.
Thank you so much for your valuable time spending here.
Have a great day.
All is well.
Regards: @meta007
