
[Image1]
Introduction
Hey it's a me again @drifter1!
Today we continue with my mathematics series about Signals and Systems in order to cover Sinusoidal and Complex Exponential Signals.
So, without further ado, let's get straight into it!
Sinusoidal Signals
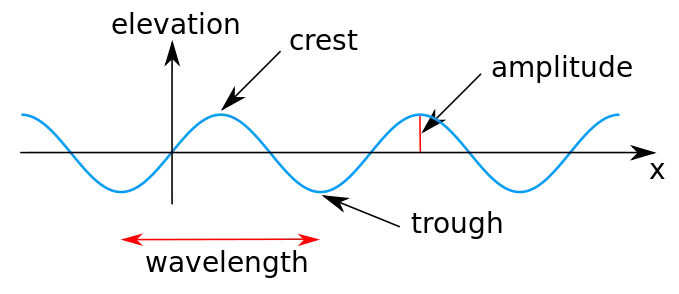
[Image 2]
Sinusoidal signals are periodic signals, which are based on the trigonometric functions sine (sin) and cosine (cos).
Continuous-Time Sinusoidals
In continuous-time, the generic form of a sinusoidal signal is:

where:
- A: amplitude
- ωo: angular frequency
- φ: phase shift
Period
The period of a sinusoidal signal is given by:
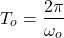
Present Ampltiude
The signal's amplitude at present (time = to = 0) can be easily calculated using:

because only the phase shift φ affects the present value.
Time Shift - Phase Shift Relationship
Time shifting a sinusoidal signal is related to phase shifting as follows:

Thus, in this example, the time shift by to is equal to a phase shift by φ = ωoto.
Or, the other way around, a phase shift by any φ implies a time shift by some unknown multiple of ωo.
Even Sinusoidal
When the phase shift is φ = 0, the sinusoidal signal A cos ωot is falling into the even category.
For a signal to be even the following must be true: x(t) = x(-t), which is of course true for the cosine function, as:
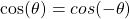
Odd Sinusoidal
In a similar way, its also possible to prove that the sine function is odd, because:
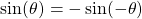
Thus, the signal A sin ωot is considered an odd signal.
Its worth noting that the sine and cosine functions/signals differ by φ = -π/2.
So, its easy to conclude that phase shifting by φ = -π/2, the cosine signal is also considered an odd signal:
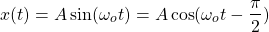
Discrete-Time Sinusoidals
In discrete-time, the sinusoidal signal is given by:

where:
- A: amplitude
- Ωo: angular frequency
- φ: phase shift
Time Shift - Phase Shift Relationship
In the case of discrete-time, time shifting again implies a phase shift:

So, a time shift by no samples is equal to a phase shift by Ωono.
Let's note that phase shifting now doesn't imply a time shift, as the sample rate affects the outcome of phase shifting.
As a result:
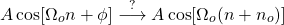
Even-Odd Sinusoidal
Similar to continuous-time, the cosine signal is again considered an even signal, whilst the sine signal an odd signal:

Requirements for Periodicity
Any sinusoidal signal is considered an periodic signal in continuous-time, but in discrete-time things change slightly.
In general, in discrete-time a signal is considered periodic only when their exists a small integer N for which:
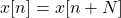
In discrete-time, a sinusoidal signal:

is periodic when ΩoN is a multiple of 2π, and so the following is true:
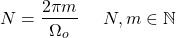
The period N is the smallest natural number for which this equation is true.
If none exists then the sinusoidal is aperiodic.
The following is a visualization of how the sample-rate affects the periodicity of a sinusoidal signal:

[Image 3]
Sinusoidals in Continuous- and Discrete-time at Distinct Frequencies
In addition to the issue of periodicity, continuous- and discrete-time sinusoidal also differ in other aspects.
In continuous-time, distinct values of the frequency ωo result into completely distinct signals. However, in discrete-time, values of Ωo which are separated by 2π result into identical signals.
So, in continuous-time, if ω2 ≠ ω1 then x2(t) ≠ x1(t). But, in discrete-time, if Ω2 = Ω1 + 2πm then x2[n] ≠ x1[n].
Exponential Signals
Exponential signals can be defined as:

where both C and a are real numbers.
Time Shift - Scale Change Relationship
Time shifting an exponential signal implies scale change, as follows:

Complex Exponentials
Replacing C and a with complex numbers results in complex explonentials, which can be easily related to sinusoidal signals using Euler's relation.
Continuous-Time
In continuous-time, an complex exponential is defined as:
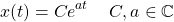
where C and a tend to be defined as:
which results in the following representation for complex exponentials:
Euler's relation allows us to replace the second exponential with a sum of cosine and sine:
And so, the final representation of complex exponentials is:
where the real and imaginary parts are clearly separated.
Complex exponentials can be thought of as exponentially growing or decaying sinusoidal signals, as shown below.

[Image 4]
Discrete-Time
In discrete-time, an complex exponential is defined as:
where C and a are defined as:
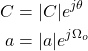
therefore resulting into the following representation:
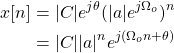
Using Euler's relation, the last exponential can be replaced by sinusoidal signals, giving us the following, now final, form:

RESOURCES:
References
- Alan Oppenheim. RES.6-007 Signals and Systems. Spring 2011. Massachusetts Institute of Technology: MIT OpenCourseWare, License: Creative Commons BY-NC-SA.
- https://www.tutorialspoint.com/signals_and_systems/
Images
Mathematical equations used in this article, where made using quicklatex.
Previous articles of the series
- Introduction → Signals, Systems
- Signal Basics → Signal Categorization, Basic Signal Types
- Signal Operations with Examples → Amplitude and Time Operations, Examples
- System Classification with Examples → System Classifications and Properties, Examples
Final words | Next up
And this is actually it for today's post! Till next time!
See Ya!

Keep on drifting!



