[Image1]
Introduction
Hey it's a me again @drifter1!
Today we continue with my mathematics series about Signals and Systems to talk about LTI System Analysis using Z Transform.
So, without further ado, let's dive straight into it!
LTI System Properties and Z Transform
Similar to the Laplace Transform, one important application of the Z Transform is again its use in LTI System analysis, representation and classification.
This property is a direct consequence of the convolution property, which it inherits from the Fourier Transform (reminder: The Z Transform is a generalization of the Discrete-Time Fourier Transform).
Due to this property, the output of a given system can be calculated using multiplication instead of convolution.
The Z Transform of the input is multiplied by the Z Transform of the system impulse response, known as the system or transfer function, giving the Z Transform of the output.
Afterwards, a simple Inverse Z Transform calculation is needed in order to calculate the output in the Time-Domain.
Mathematically:
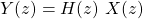
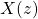 : Z Transform of the system input
: Z Transform of the system input : Z Transform of the system output
: Z Transform of the system output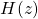 : Z Transform of the system impulse response (system or transfer function)
: Z Transform of the system impulse response (system or transfer function)
As with the Laplace Transform, this algebraic representation of system is not sufficient in the case of the Z Transform. A given system cannot be represented purely by its system function H(z), or even its block diagram, but the Region of Convergence (short ROC) is also quite important to define. Many properties of LTI systems are analyzed in correlation to the ROC of the system function, and characteristics of the poles and zeros.
Causality
First, let's get into the property known as causality...
A system is considered to be causal, when its response/output only depends on past and present input. As such, causal LTI systems have zero impulse response (h[n] = 0) for t < 0, and are right-sided.
In the case of the Z Transform, we know that the ROC is related to circles in the complex plane. This means, that the ROC of a causal system is the outside region of circle. If h[n] = δ[n] then H(z) = 1, and so the ROC can be expanded to possibly include the initial point (n = 0). Being a right-sided impulse response, the ROC might even include the infinity point, if the power series has no positive z exponents.
So, let's summarize all this into a property:
A Discrete-Time LTI system is causal, only and only if the ROC of its system function is the outside region of a circle, possibly even including points at infinity.
Let's get even more-in-depth now, by considering that the system function is rational. In that case, the ROC will have to be outside of the most distant pole, and include infinity. In other words, the limit of H(z) to infinity must be finite. A limit of a ratio is finite, if the degree of the numerator is smaller or equal to teh degree of the denominator. As such, if H(z) is represented as a ratio of polynomials of z, we can specify the following property:
A Discrete-Time LTI system with rational system function is causal, only and only if (1) the ROC is the outside region of a circle outisde of the most distance pole, and (2) the degree of the numerator polynomial is not larger then the degree of the denominator polynomial
Stability
Now, let's get into stability...
A system is considered stable if bounded input leads to bounded output. So, finite amplitude input leads to finite amplitude output, meaning that the system impulse response is absolutely integratable. In the case of the Z Transform, this is quite simple to achieve, giving us the following property:
An Discrete-Time LTI system is stable only and only if the ROC of the system function contains the unit circle, |z| = 1.
In the case of a rational system function, if the system is already proven to be causal, its also possible to prove stability by simply checking the pole positions. For the system to be causal its ROC is the outside region of a circle outside of the most distance pole, and for it to also be causal, the poles must all be inside of the unit circle (pole amplitude < 1). Let's summarize this into a property:
An causal Discrete-Time LTI system with rational system function is also stable, only and only if, all the poles of the system function are within the unit circle, that is the poles have an ampltitude of less than 1.
LCCDE Representation and Z Transform
The properties of the Z Transform, make this Transform particularly useful for the sake of analyzing LTI systems. As we already seen before, Discrete-Time LTI systems can be represented using linear constant-coefficient difference equations (short LCCDE). As such, when the Z Transform is applied to such an difference equation, the equation is converted into a far simpler algebraic expression. This expression relates the Z Transform of the system output with the product of the Laplace Transform of the system input and the system function. And, the system response can then be taken by using the Inverse Z Transform.
As a small recap, this is how such LCCDEs are represented:

Taking the Z Transform of both sides, and using the linearity and time-shifting properties, yields:

And so, the ratio, which is the system function, is:

So, these two sums, are basically the zero and pole polynomials. The roots of the numerator give us the zeros of the system function, whilst the roots of the denominator give us the poles. Of course, the LCCDE doesn't specify the ROC, and so properties such as stability or causality need to be used in order to specify the exact ROC!
RESOURCES:
References
Images
Mathematical equations used in this article were made using quicklatex.
Block diagrams and other visualizations were made using draw.io and GeoGebra
Previous articles of the series
Basics
- Introduction → Signals, Systems
- Signal Basics → Signal Categorization, Basic Signal Types
- Signal Operations with Examples → Amplitude and Time Operations, Examples
- System Classification with Examples → System Classifications and Properties, Examples
- Sinusoidal and Complex Exponential Signals → Sinusoidal and Exponential Signals in Continuous and Discrete Time
LTI Systems and Convolution
- LTI System Response and Convolution → Linear System Interconnection (Cascade, Parallel, Feedback), Delayed Impulses, Convolution Sum and Integral
- LTI Convolution Properties → Commutative, Associative and Distributive Properties of LTI Convolution
- System Representation in Discrete-Time using Difference Equations → Linear Constant-Coefficient Difference Equations, Block Diagram Representation (Direct Form I and II)
- System Representation in Continuous-Time using Differential Equations → Linear Constant-Coefficient Differential Equations, Block Diagram Representation (Direct Form I and II)
- Exercises on LTI System Properties → Superposition, Impulse Response and System Classification Examples
- Exercise on Convolution → Discrete-Time Convolution Example with the help of visualizations
- Exercises on System Representation using Difference Equations → Simple Block Diagram to LCCDE Example, Direct Form I, II and LCCDE Example
- Exercises on System Representation using Differential Equations → Equation to Block Diagram Example, Direct Form I to Equation Example
Fourier Series and Transform
- Continuous-Time Periodic Signals & Fourier Series → Input Decomposition, Fourier Series, Analysis and Synthesis
- Continuous-Time Aperiodic Signals & Fourier Transform → Aperiodic Signals, Envelope Representation, Fourier and Inverse Fourier Transforms, Fourier Transform for Periodic Signals
- Continuous-Time Fourier Transform Properties → Linearity, Time-Shifting (Translation), Conjugate Symmetry, Time and Frequency Scaling, Duality, Differentiation and Integration, Parseval's Relation, Convolution and Multiplication Properties
- Discrete-Time Fourier Series & Transform → Getting into Discrete-Time, Fourier Series and Transform, Synthesis and Analysis Equations
- Discrete-Time Fourier Transform Properties → Differences with Continuous-Time, Periodicity, Linearity, Time and Frequency Shifting, Conjugate Summetry, Differencing and Accumulation, Time Reversal and Expansion, Differentation in Frequency, Convolution and Multiplication, Dualities
- Exercises on Continuous-Time Fourier Series → Fourier Series Coefficients Calculation from Signal Equation, Signal Graph
- Exercises on Continuous-Time Fourier Transform → Fourier Transform from Signal Graph and Equation, Output of LTI System
- Exercises on Discrete-Time Fourier Series and Transform → Fourier Series Coefficient, Fourier Transform Calculation and LTI System Output
Filtering, Sampling, Modulation, Interpolation
- Filtering → Convolution Property, Ideal Filters, Series R-C Circuit and Moving Average Filter Approximations
- Continuous-Time Modulation → Getting into Modulation, AM and FM, Demodulation
- Discrete-Time Modulation → Applications, Carriers, Modulation/Demodulation, Time-Division Multiplexing
- Sampling → Sampling Theorem, Sampling, Reconstruction and Aliasing
- Interpolation → Reconstruction Procedure, Interpolation (Band-limited, Zero-order hold, First-order hold)
- Processing Continuous-Time Signals as Discrete-Time Signals → C/D and D/C Conversion, Discrete-Time Processing
- Discrete-Time Sampling → Discrete-Time (or Frequency Domain) Sampling, Downsampling / Decimation, Upsampling
- Exercises on Filtering → Filter Properties, Type and Output
- Exercises on Modulation → CT and DT Modulation Examples
- Exercises on Sampling and Interpolation → Graphical/Visual Sampling and Interpolation Examples
Laplace and Z Transforms
- Laplace Transform → Laplace Transform, Region of Convergence (ROC)
- Laplace Transform Properties → Linearity, Time- and Frequency-Shifting, Time-Scaling, Complex Conjugation, Multiplication and Convolution, Differentation in Time- and Frequency-Domain, Integration in Time-Domain, Initial and Final Value Theorems
- LTI System Analysis using Laplace Transform → System Properties (Causality, Stability) and ROC, LCCDE Representation and Laplace Transform, First-Order and Second-Order System Analysis
- Exercises on the Laplace Transform → Laplace Transform and ROC Examples, LTI System Analysis Example
- Z Transform → Z Transform, Region of Convergence (ROC), Inverse Z Transform
- Z Transform Properties → Linearity, Time-Shifting, Time-Scaling, Time-Reversal, z-Domain Scaling, Conjugation, Convolution, Differentation in the z-Domain, Initial and Final value Theorems
Final words | Next up
And this is actually it for today's post!
Next time we will get into full-on exercises on the Z Transform...and its usefulness in LTI System Analysis!
See Ya!

Keep on drifting!

