
[Image1]
Introduction
Hey it's a me again @drifter1!
Today we continue with my mathematics series about Signals and Systems to get into Linear Feedback Systems.
So, without further ado, let's dive straight into it!
Introduction to Feedback
The concepts that we've covered throughout this series are sufficient for the basic analysis of linear feedback systems. But, let's first try to understand what Feedback is and why it's so useful.
Feedback is something that sometimes even comes naturally, like the audio speaker feeding back to the microphone. Too strong of a feedback leads to system instability (distortion in the case of mics). But, just the right amount can be useful for controlling or enhancing the system performance. Feedback applications include:
- Amplifier design : compensate for uncertainties in element characteristics such as the frequency response.
- Stabilizing unstable systems
- in a control system some disturbances and parameters might not be specified accurately.
- use error signal to find and minimize between the desired and actual value.
- when using feedback the system is less-sensitive then an open-loop control system
In modern control systems, digital, and thus discrete-time, feedback systems are used.
Linear Feedback System Analysis
In the case of continuous-time LF systems, the main analysis tool is the Laplace transform, whilst in the case of discrete-time LF system it's the Z-Transform. Either way, in both cases the so called basic feedback equation describes the overall system function of a feedback system in terms of two paths:
- forward path (system response)
- feedback path (system feedback)
Suppose H(s) is the forward path equation and G(s) the feedback path equation, then a basic feedback system can be visualized graphically as follows:

Or mathematically, the system feedback equation of this continuous-time LF system is:

In the case of discrete-time, s simply changes into z.
There are different conditions for stability in C-T and D-T:
- a continuous-time system must have all of its poles in the left-half s-plane
- a discrete-tiem system must have all of its poles inside of the unit circle
Mathematically, these conditions can be written as:
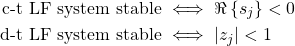
From these conditions it's also possible to come to the conclusion that the combined gain of the forward and feedback paths must be less than unity (1). Thus, if K1 and K2 are the forward and feedback path gains respectively, then:

RESOURCES:
References
Images
Mathematical equations used in this article were made using quicklatex.
Block diagrams and other visualizations were made using draw.io
Previous articles of the series
Basics
- Introduction → Signals, Systems
- Signal Basics → Signal Categorization, Basic Signal Types
- Signal Operations with Examples → Amplitude and Time Operations, Examples
- System Classification with Examples → System Classifications and Properties, Examples
- Sinusoidal and Complex Exponential Signals → Sinusoidal and Exponential Signals in Continuous and Discrete Time
LTI Systems and Convolution
- LTI System Response and Convolution → Linear System Interconnection (Cascade, Parallel, Feedback), Delayed Impulses, Convolution Sum and Integral
- LTI Convolution Properties → Commutative, Associative and Distributive Properties of LTI Convolution
- System Representation in Discrete-Time using Difference Equations → Linear Constant-Coefficient Difference Equations, Block Diagram Representation (Direct Form I and II)
- System Representation in Continuous-Time using Differential Equations → Linear Constant-Coefficient Differential Equations, Block Diagram Representation (Direct Form I and II)
- Exercises on LTI System Properties → Superposition, Impulse Response and System Classification Examples
- Exercise on Convolution → Discrete-Time Convolution Example with the help of visualizations
- Exercises on System Representation using Difference Equations → Simple Block Diagram to LCCDE Example, Direct Form I, II and LCCDE Example
- Exercises on System Representation using Differential Equations → Equation to Block Diagram Example, Direct Form I to Equation Example
Fourier Series and Transform
- Continuous-Time Periodic Signals & Fourier Series → Input Decomposition, Fourier Series, Analysis and Synthesis
- Continuous-Time Aperiodic Signals & Fourier Transform → Aperiodic Signals, Envelope Representation, Fourier and Inverse Fourier Transforms, Fourier Transform for Periodic Signals
- Continuous-Time Fourier Transform Properties → Linearity, Time-Shifting (Translation), Conjugate Symmetry, Time and Frequency Scaling, Duality, Differentiation and Integration, Parseval's Relation, Convolution and Multiplication Properties
- Discrete-Time Fourier Series & Transform → Getting into Discrete-Time, Fourier Series and Transform, Synthesis and Analysis Equations
- Discrete-Time Fourier Transform Properties → Differences with Continuous-Time, Periodicity, Linearity, Time and Frequency Shifting, Conjugate Symmetry, Differencing and Accumulation, Time Reversal and Expansion, Differentation in Frequency, Convolution and Multiplication, Dualities
- Exercises on Continuous-Time Fourier Series → Fourier Series Coefficients Calculation from Signal Equation, Signal Graph
- Exercises on Continuous-Time Fourier Transform → Fourier Transform from Signal Graph and Equation, Output of LTI System
- Exercises on Discrete-Time Fourier Series and Transform → Fourier Series Coefficient, Fourier Transform Calculation and LTI System Output
Filtering, Sampling, Modulation, Interpolation
- Filtering → Convolution Property, Ideal Filters, Series R-C Circuit and Moving Average Filter Approximations
- Continuous-Time Modulation → Getting into Modulation, AM and FM, Demodulation
- Discrete-Time Modulation → Applications, Carriers, Modulation/Demodulation, Time-Division Multiplexing
- Sampling → Sampling Theorem, Sampling, Reconstruction and Aliasing
- Interpolation → Reconstruction Procedure, Interpolation (Band-limited, Zero-order hold, First-order hold)
- Processing Continuous-Time Signals as Discrete-Time Signals → C/D and D/C Conversion, Discrete-Time Processing
- Discrete-Time Sampling → Discrete-Time (or Frequency Domain) Sampling, Downsampling / Decimation, Upsampling
- Exercises on Filtering → Filter Properties, Type and Output
- Exercises on Modulation → CT and DT Modulation Examples
- Exercises on Sampling and Interpolation → Graphical/Visual Sampling and Interpolation Examples
Laplace and Z Transforms
- Laplace Transform → Laplace Transform, Region of Convergence (ROC)
- Laplace Transform Properties → Linearity, Time- and Frequency-Shifting, Time-Scaling, Complex Conjugation, Multiplication and Convolution, Differentation in Time- and Frequency-Domain, Integration in Time-Domain, Initial and Final Value Theorems
- LTI System Analysis using Laplace Transform → System Properties (Causality, Stability) and ROC, LCCDE Representation and Laplace Transform, First-Order and Second-Order System Analysis
- Exercises on the Laplace Transform → Laplace Transform and ROC Examples, LTI System Analysis Example
- Z Transform → Z Transform, Region of Convergence (ROC), Inverse Z Transform
- Z Transform Properties → Linearity, Time-Shifting, Time-Scaling, Time-Reversal, z-Domain Scaling, Conjugation, Convolution, Differentation in the z-Domain, Initial and Final value Theorems
- LTI System Analysis using Z Transform → System Properties (Causality, Stability), LCCDE Representation and Z Transform
- Exercises on the Z Transform → Z Transform and ROC Examples, ROC from Conditions, LTI System Analysis Example
- Continuous-Time to Discrete-Time Design Mapping → Discrete-Time System Design Techniques (Mapping from Derivatives to Differences, Mapping using Impulse Invariance), First- and Second-Order Systems and Z-Transform
- Butterworth Filters → Butterworth Filter Parameters, Equation and Pole-Zero Plot, Mapping using Impulse-Invariance and Bilinear Transformation
Final words | Next up
And this is actually it for today's post!
Next up will be System Feedback Exercises...
See Ya!

Keep on drifting!

