Hi there. In this mathematics post, I provide an overview of piecewise functions. This post is theoretical and mathematical in nature but I do think it is nice to understand some of the logic behind piecewise functions. There are more scenarios than you think where there are outcomes based on different inputs depending on the situation when it comes to life, gambling and decision making.
The stuff in this post is based on stuff I have seen and learned when I was a math student. Note that there are more piecewise functions and variations than covered here. This post is technical.
Math text and images rendered with the use of Quicklatex.com. I also use Desmos to show piecewise function graphs.

Topics
- Basic Idea Of Piecewise Functions
- True or False as in Zero or One
- Having More Than 2 Outputs
- Absolute Value Function
- Heaviside Function
- Dirichlet Function
- Probability Functions
- Indicator Functions
- Max & Min Functions
- Finance Example - Call Options, Put Options For Stocks
Basic Idea Of Piecewise Functions
Piecewise functions at first kind of look weird. Do consider a vending machine. You input a certain amount of money and choose a product. If there is enough money for the product the condition is met and the vending machine outputs the desired product. A piecewise function takes an input and produces an output depending on the input.
For programmers, piecewise functions are very similar to if-then statements.

True or False as in Zero or One
One of the basic piecewise functions out there is one that outputs zero or one depending on the input. Here is one example.

You could also do a True/False case:
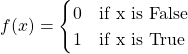
Having More Than 2 Outputs
Piecewise functions can have more than two outputs depending on the input. Here is an example where there are 3 outputs that depend on the inputs.

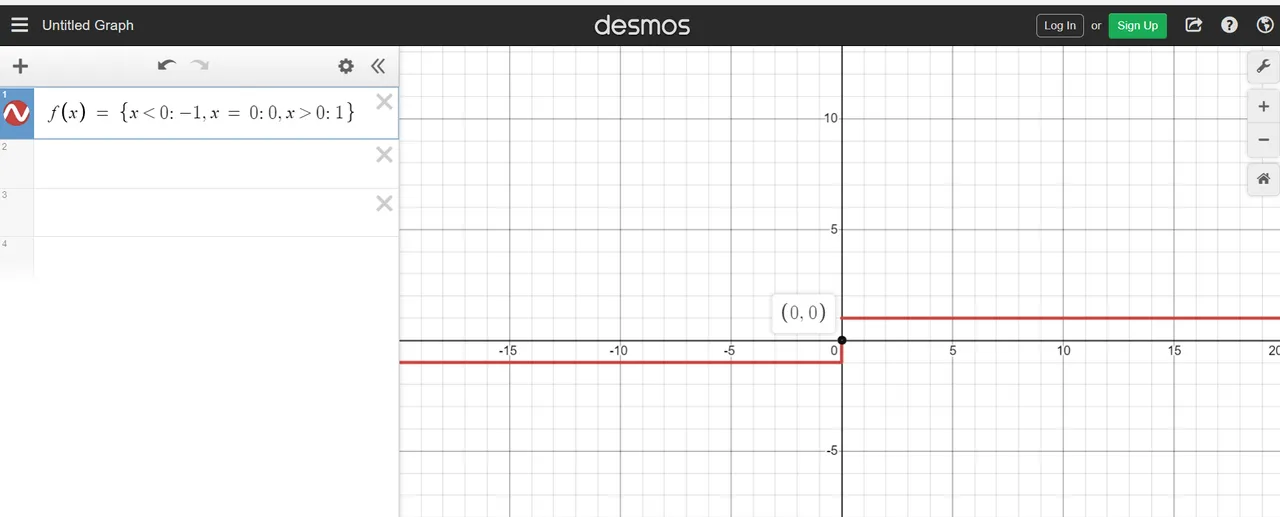
Absolute Value Function
The absolute value function is a piecewise function that combines two linear functions. The linear function depends on the input for x. The absolute value of a negative number is positive and the absolute value of a positive number is positive. You can view the absolute value as the distance of the given number to 0.

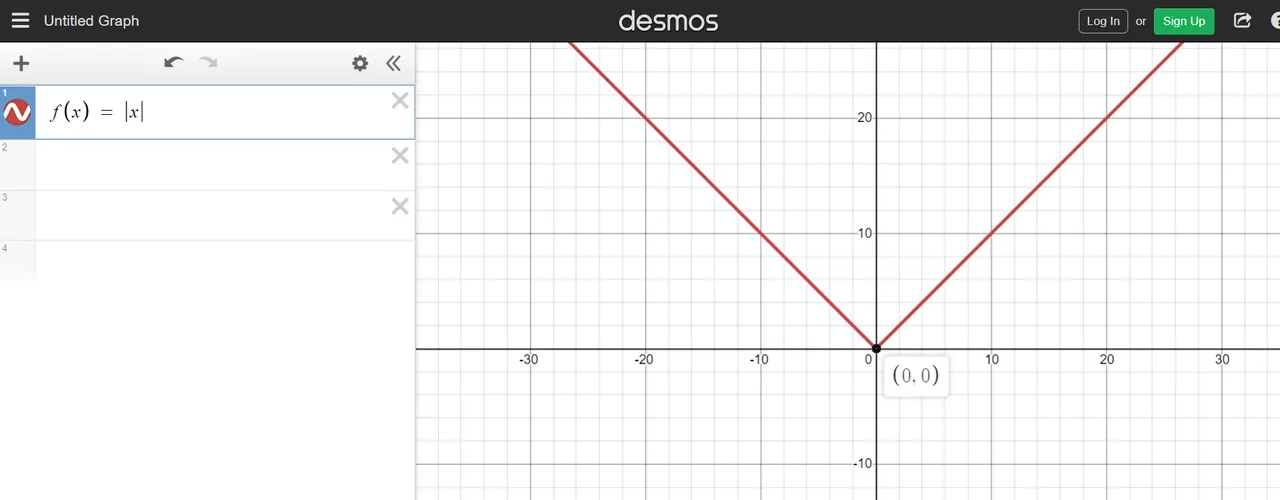
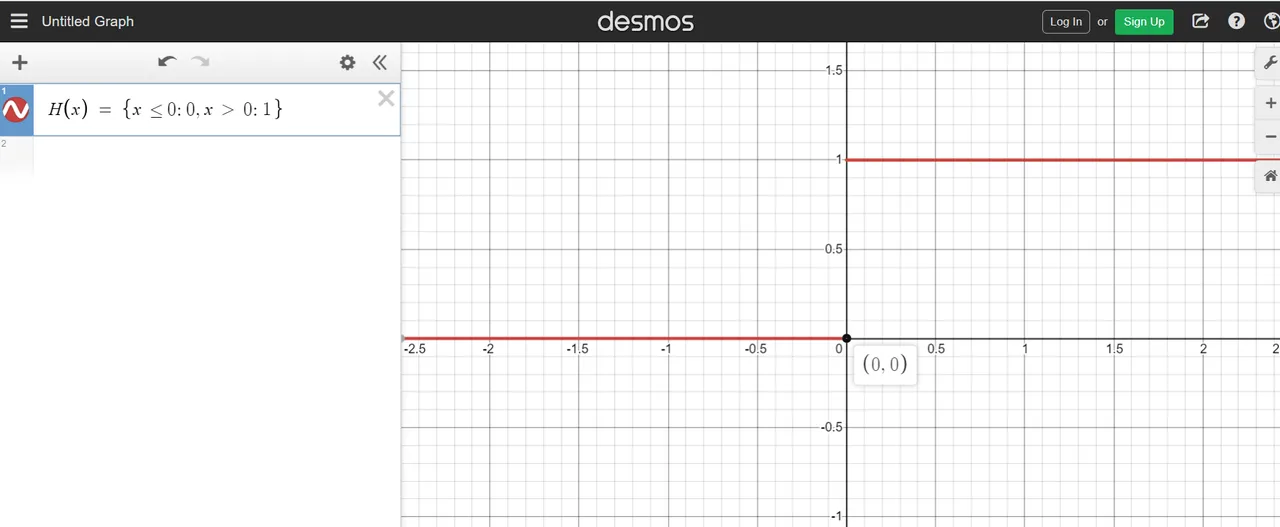
Heaviside Function
The Heaviside function is sometimes known as a step function. As this function may appear simple, it does appear in calculus, differential equations and in probability theory.

Dirichlet Function
Depending on the input for the Dirichlet function, the output is 0 or 1. If the input number is a rational number the output is 1. An irrational number such as pi, sqrt(2) would output a zero. The set of rational numbers is denoted by the math text Q.

Probability Functions
At the higher levels, probability include ideas from calculus. According to Investopedia (a finance website), a probability distribution is a statistical function that has values and likelihoods that a random variable can take. You can view a (continuous) probability distribution as a smoothed out version of a histogram.

One well known probability distribution is the normal distribution. This normal distribution is sometimes referred to the Gaussian distribution as it is named after the German mathematician Carl Friedrich Gauss.
The normal distribution is actually not a piecewise function. Other probability distributions can be written in the form of a piecewise function. One example of a probability distribution function that can be a piecewise function is the exponential distribution.
Exponential Distribution In Probability
The standard exponential distribution in probability has the equation of the form:

As this function is defined for non-negative values of x, the above can be rewritten as a piecewise function.

Reference: https://www.itl.nist.gov/div898/handbook/eda/section3/eda3667.htm
Indicator Functions
My first encounter with indicator functions was from this math professor in a first course in probability and statistics at second year university. This topic was not that difficult to grasp but the notation did confuse quite a few people.
The indicator function is simply a piecewise function. This function is sometimes called a characteristic function. It can be used in probability theory as the probability can be zero depending on the input.

If the element x is in the set A, the indicator function is a 1. This 1 is like a TRUE. If the element x is not in A, the indicator function outputs a 0 as a false.
Dirichlet Function As An Indicator Function
An example of an indicator function was already shown before in this post in the form of the Dirichlet function. If x is a rational number you have a 1. A zero appears if x is not a rational number (irrational).

Exponential Distribution With An Indicator Function
With the exponential probability distribution we had:

If an indicator function is used we would have:


Max & Min Functions
Maximum and minimum functions are interesting functions in their own right. These max and min function are actually piecewise functions as the chosen output depends on the input value.
Maximum functions choose the largest value given multiple inputs. Minimum functions choose the lowest value given two or more inputs.
Simple Example

The above examples are very to follow and you may wonder what does it have to do with piecewise functions. Check out this next example.
Adding A Variable To Max & Min
What if the inputs to a max function are 0 and x? The value of x is unknown. If x is greater than zero, then the maximum of 0 and x is x. If x less than zero the maximum of 0 and x is 0. This leads to this piecewise function.


Here is the piecewise function for the minimum function for the inputs of 0 and x. Zero is outputted if x is greater than 0 and x appears if 0 is higher than x.


Maximum of x and y
This example is upping the difficulty. What if the two inputs are unknown values if the form of x and y. Think in cases again when it comes to constructing the piecewise function here. If x is higher than y, choose x. For the case of y being greater than x choose y. If both values are equal you can choose one or the other.

The minimum case can be done as an exercise. I did not cover 3 or more inputs here.
Finance Example - Call Options, Put Options For Stocks
I thought that I would throw in an extension and example in one. I know some things about finance from the math perspective. Call options and put options are financial products that belong to the financial derivatives class. These options depend on the price of the underlying stock.
Call Option
A call option gives the holder the right not the obligation to purchase 100 shares of the underlying stock at a strike price K at the expiry date . (I assume European options and not American options.) If the stock price for XYZ goes above K, the call option can be exercised. The 100 shares can be bought at the lower price of K and then these same 100 shared can be sold at the price above K for a profit.
This payoff can be expressed as a max function and as a piecewise function.

If the stock price at expiry S(T) is higher than the strike price K, the call option is exercised. Shares are bought cheaper at price K and can be sold at a profit. In the event of the stock price being lower than strike price K, the call option is not exercised. The loss is the cost of the option premium price.

Source: https://www.optionsbro.com/long-call-option-strategy-example/
Put Option
While a call option deals with the buying case, a put option gives the contract holder the right but not the obligation to sell 100 shares of the underlying stock at a strike price K. You hope that the price of the stock falls such that you can sell at a higher strike price K.


Source: https://www.theoptionsguide.com/long-put.aspx
The above two cases dealt with buying options. There is also selling options which is not covered here.
That is my overview on piecewise functions. There are simple cases and there are some more complicated cases. The main takeaway with piecewise functions is that outputs can vary depending on the inputs for the function. There are if statements involved.
