Alright so it basically took me like an hour to hash this out so I figured I might as well share with the class.
https://blog.bancor.network/beginners-guide-to-getting-rekt-by-impermanent-loss-7c9510cb2f22
Essentially if you provide liquidity to a Uniswap pool (AMM Automated-Market-Maker algorithm) you'll suffer something called "impermanent loss" if the value of the underlying assets change. If the underlying asset's value returns to "normal" you'll recapture those "temporary" "losses".
For simplicity I'll use the DAI/ETH pool as an example so we can assume a constant $1 value for DAI and eliminate that side of the equation.

The reason it took me so long to understand this concept of impermanent losses is because I actually already figured it out on my own without doing the research on it. However, the conclusions I made in those posts a few weeks back ran contradictory to what I was reading today. What are the chances that I'm right and everyone else is wrong? Not good.
Definition
The precise definition of impermanent loss is very important. It's actually quite simple. Impermanent loss in the difference between your holdings as an LP provider VS simply holding those same assets in a wallet (not for sale & no fees collected).
Examples: Uniswap as hedge.
I used the extreme example of ETH either going x4 or losing 75% of its value. This makes the numbers easy. When ETH goes x4 the Uniswap pool halves the current amount of ETH, and doubles the supply of DAI because users are dumping DAI into the pool to swap for ETH. Conversely, when ETH loses 75% value users are dumping their ETH and buying DAI, increasing ETH by double and decreasing DAI by half.
In this scenario, if ETH crashes 75% an LP provider only loses 50% of their value, while if ETH goes x4 they only gain x2. Therefore, I concluded being an LP provider to this pool helps lower volatility and save money in the long run (contrary to this whole concept of impermanent losses).
This graph assumes $100 ETH starting value.
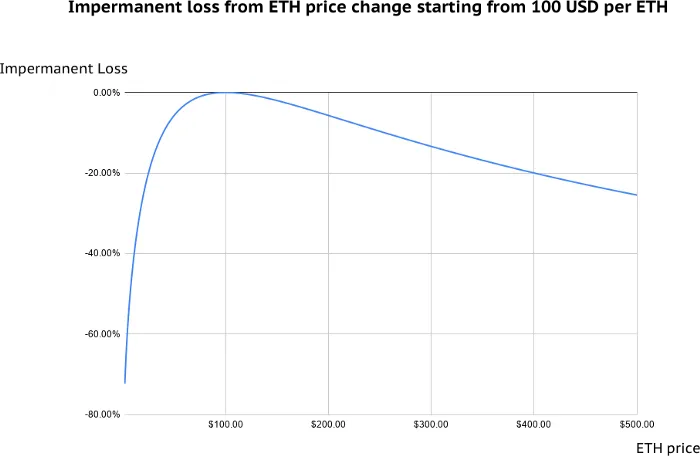
When presented with this new information I was extremely confused. This clearly shows that if ETH goes x4 or drops 75%, LP providers will suffer 20% impermanent loss no matter what. These numbers made very little sense to me in the context that I had previously come to understand the issue.
This confusion was caused by the definition of impermanent loss, which compares the assets being held within LP tokens against those contained inside a liquid wallet. Meanwhile, I was comparing someone who was holding 100% of their assets in ETH vs the LP provider (half of who's value lies in a stable coin).
For example, say ETH crashes 75% and I had $2000 in the DAI/ETH pool. After the crash my LP tokens would now be worth $1000, while someone with $2000 worth of ETH would be sucking down a $1500 loss down to a total value of $500. However, impermanent loss looks at someone who was holding $1000 worth of ETH and 1000 DAI, who's value after the drop would be $1250. Therefore, these guys are making the claim that you lost $250 because your money was in the Uniswap pool.
In addition to this confusion, the number that I came up with was 25% loss and not 20% loss. Turns out, this is just a matter of perspective. The difference between $1000 and $1250 is both 25% and 20% depending on what side you're coming at it from. If you have $1000 and you could of had $1250 you missed out on a 25% gain, but if you have $1250 you avoided a 20% loss. Semantics.

This is the example that the Bancor Network Blog gives, and it is equally confusing. They are making it look like arbitrage traders are siphoning the Uniswap pool and padding their own pockets with gains acquired from the Liquidity Providers. This is 100% false and ridiculous. In this example, arbitrage traders are not "stealing" $2.38 from LPs and putting it into their own pockets.
The logical proof of this conclusion is pretty simple. If arbitrage traders were able to siphon $2.38 cents in this example as the value of ETH rises 10%, then they could also siphon ANOTHER $2.38 cents on the way back down. However, the definition of impermanent loss is just that: impermanent. When the price returns to the initial value, Liquidity Providers on Uniswap by literal definition of "impermanent" have lost zero dollars.
Therefore, how could arbitrage traders possibly be siphoning money from the LPs? Short answer: they aren't. They are in reality siphoning that value from the centralized exchange they are arbitraging and/or other Uniswap traders, not the LPs. Money from the arbitrage traders doesn't just magically appear back into the LPs pockets after the price returns to the original value. This infographic is extremely misleading, and I assume the reason for that is to promote this new Bancor Network system that attempts to mitigate the impermanent loss problem.
Bancor Protocol v2.1 suggests a new way to distribute the risk of impermanent loss insurance in order to offer single-asset exposure and higher ROI from collected fees:
https://blog.bancor.network/proposing-bancor-v2-1-single-sided-amm-with-elastic-bnt-supply-bcac9fe655b
Yeah, that's great Bancor, but in pushing your own "solution" to this "problem" you've completely muddied the waters of the issue in question. In fact, it seems that most of the articles I read on this topic have a very hard time of explaining it correctly.

"Impermanent Loss"
Even calling it that is a complete misnomer. If Bitcoin goes x2 do you run around telling all the Bitcoin holders they lost money because they didn't x10 margin trade it? No, because that would make you look like a complete jackass. In the same way that margin trading is extremely risky compared to normal trading that doesn't involve making bets with money you borrowed, being an LP on Uniswap is much less risky compared to normal trading.
LPs on Uniswap are the backbone of Uniswap. When you provide liquidity to Uniswap, you become the exchange as you bet against the market. The market wants to buy? No problem, you're selling. The market wants to sell? No problem, you're buying. And it's all done automatically via the algorithm.
So of course if you are buying the dip and selling the spike on a sliding scale all the way up and down, you're going to "take losses" compared to someone who's assets are just sitting in a wallet. That's the entire point: LPs are the mechanism of exchange. When traders win, you lose. Simple as that.
The house always wins.
Guess what? On average over time we all know that traders lose their money. Guess where that money goes? Into the pockets of the people collecting exchange fees. On Uniswap as an LP, that's you! Good deal! Trying to make it look like it's not a good thing with this whole impermanent loss thing is pretty silly.
In addition, show me that guy who holds $1000 worth of ETH and DAI in the same wallet? Where is he? I don't see him. It's a silly example because the vast majority of people out there do not maintain a balanced position. Most traders are gamblers and min/max their bets in an attempt to scoop as much gains as possible. More often than not, this strategy backfires, as most of us well know.

Trying to compare an LP provider with a trader who's holding the same assets as an LP provider is a fool's errand. You can't isolate one moment in time and then tell people they made a mistake in retrospect. That's exactly the kind of thing a BAD GAMBLER does. Spoiler alert: when you see a slot machine that hasn't hit the jackpot in a while, the chances of it hitting the jackpot do not go up. Previous outcomes of chance to not affect future outcomes of chance; that is a fact.
Here's a more realistic scenario:
Bob and Sally both have $1000 worth of ETH and DAI. Bob decides to FOMO all-in and trades his 1000 DAI for ETH. Sally enters the Uniswap pool. ETH crashes 50%, and now Bob feels trapped and hunkers down and holds, hoping his luck will change. Meanwhile, Sally still controls a bunch of DAI due to her Uniswap holdings. She exits the pool and FOMOs all in to ETH after the big dip. Now she's way farther ahead in the trading game than BOB is.
In the opposite scenario, where ETH goes x2 rather than losing 50%, the risk taken was EXACTLY the same. Bob took more risk than Sally and his stake will reflect that depending on chance.
One of the biggest problems with this concept of impermanent loss is the need for humans to isolate and simplify the variables for easier understanding.
- Are we taking into consideration that the vast majority of traders do not maintain a balanced position required by Uniswap LPs? No.
- Are we taking into consideration that LPs are yield farming exchange fees? No.
- Are we taking into consideration the psychologically adverse affects of trading vs the set-it-and-forget-it nature of Uniswap pools? No.
- Are we taking into consideration that traders do just that: trade? And each trade incurs a fee that goes directly into the LPs pocket? No.
Instead, we are simply looking back into the past, hindsight 20/20, and saying to ourselves, "Oh shit I could have made more money if... XYZ."
Coulda, woulda, shouda.
These are the thought processes of a bad gambler. Yeah, you know what would have made you even more money? Is if you correctly longed/shorted the market using x10 leverage. That doesn't mean this is the correct play, only that it is more risky. Nobody can see the future.

Conclusion
This concept of "impermanent loss" is extremely misleading right down to the title of the phenomenon. Lowering volatility is not a loss. Buying the dip slash selling the spike algorithmically is not a foolish play, it is an extremely pragmatic one that puts us in the drivers seat as partial owner of the exchange. It is decentralization at its finest.
Anyone who says otherwise either does not fully understand the issue or suffers from the commonly extreme FOMO in this space that leads to gambling addiction. I know the feeling; We all do.
Of course, that being said, it is good to know that this issue exists, as many clearly do not. What do people think, that they can charge exchange fees and farm the Uniswap pool without actually trading the assets they put into the pool? I suppose that must be the case. Just remember: as a Uniswap LP you're betting against the market; you are the house. Traders win, you lose. Good thing for us that traders always lose on average over time as a whole. That is a mathematical fact.
