Hello math bugs(🐞) and Hivers(🐝)
I hope you all are strong and stout.
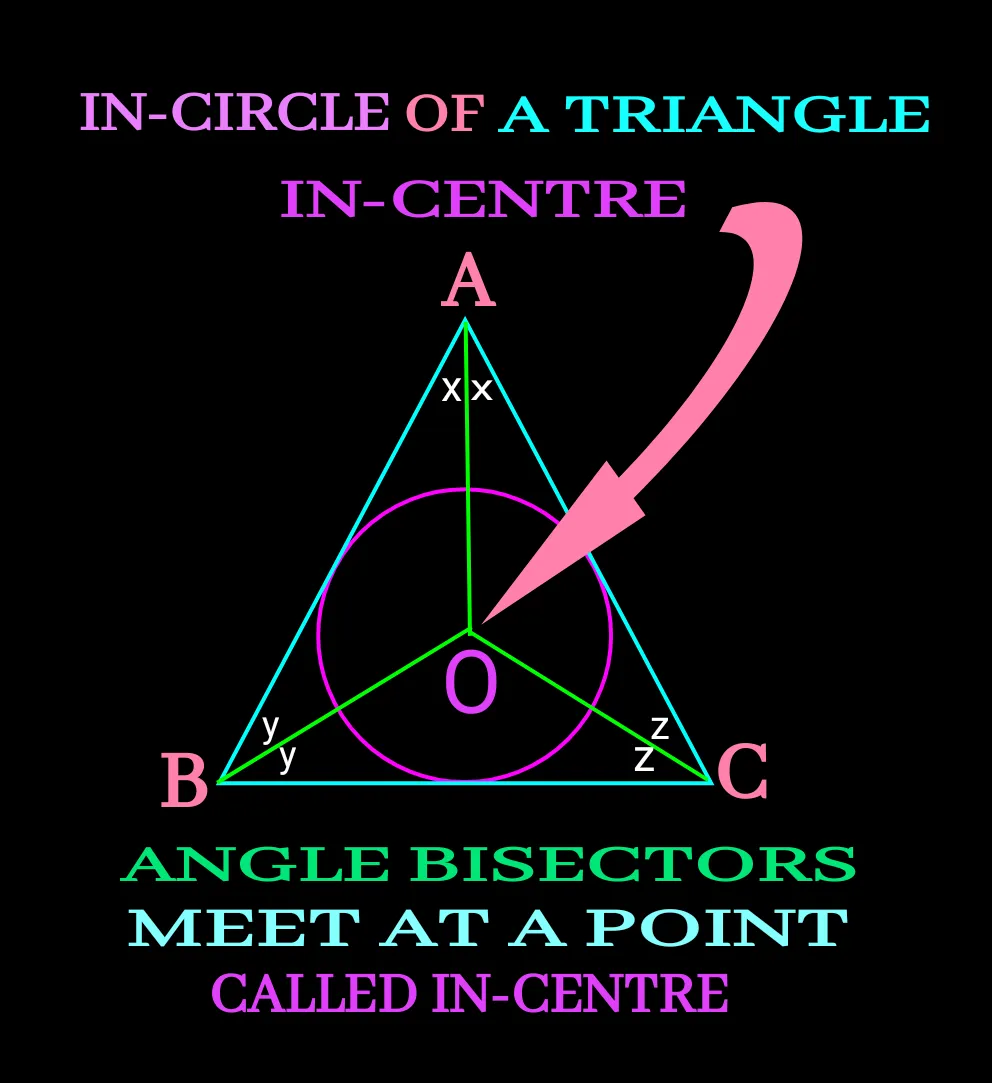
My last post was about cir-cim-circle and today I have come up with in-circle and its properties.
We can take any kind of triangle and if we bisects any two angles, the bisectors will meet a point always inside the triangle and the point is called in centre. We can also draw three bisectors of the three angle of a triangle. The sides of the taken triangle are always equidistance from the IN-CENTRE and the distance is called in-radius. Hence taking the radius if we draw a circle ,it will thus be an in-circle the triangle.
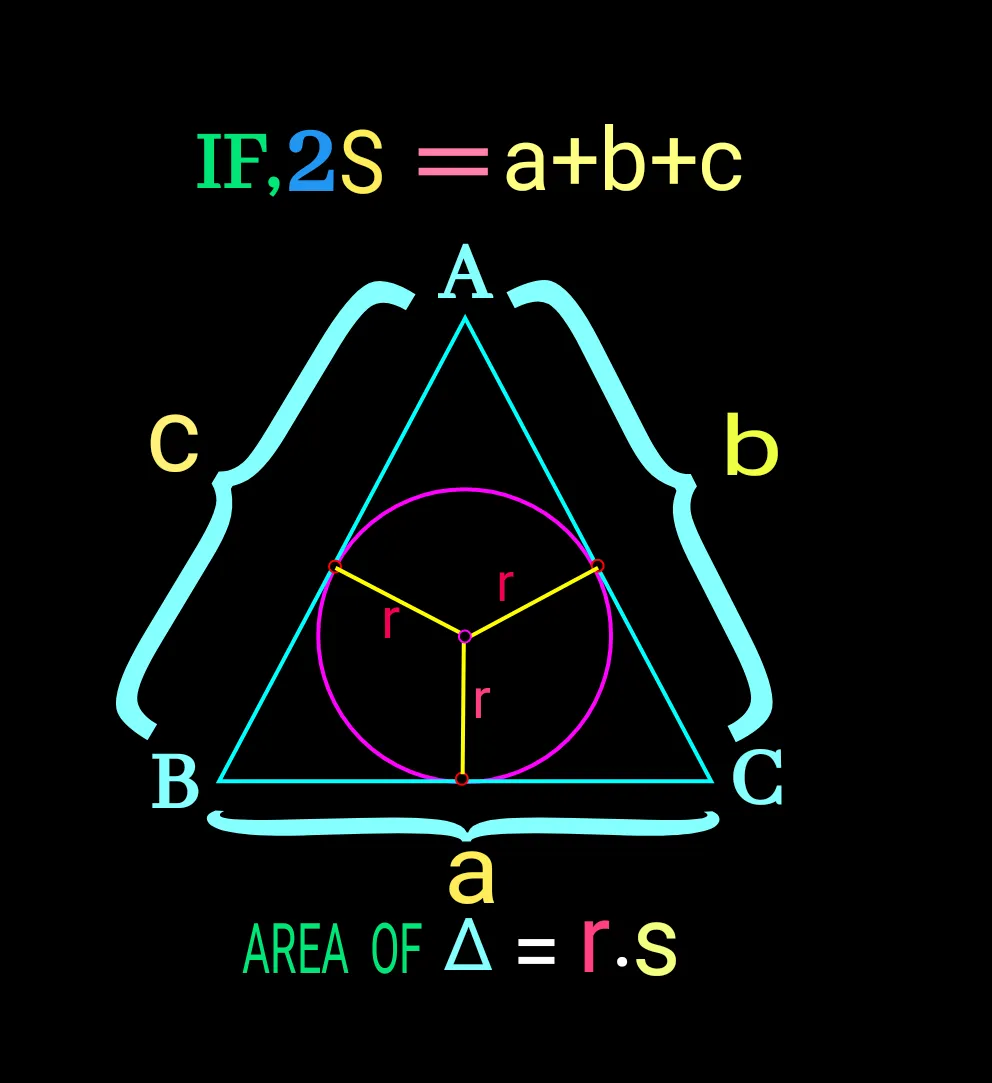
If the length of perimeter of the triangle be 2S
Then semi-perimeter (S)= (a+b+c)/2
Hence,
Area of the ∆ABC in the figure below is (∆) = r.s
Check it below:
Things to be considered:
- The triangle may be equilateral, isosceles, scalance is all cases unlike cir-cum-circle the in-centre is always inside the triangle.The same is for right angle triangle also.
- It is not necessary a in-radius touch a side of a triangle on the mid point. In case of equilateral triangle it touches the mid point.
- It is not necessary the angle bisectors touch vertices of a circle though in case of equilateral triangle it touches.
Find the area of the following triangle:
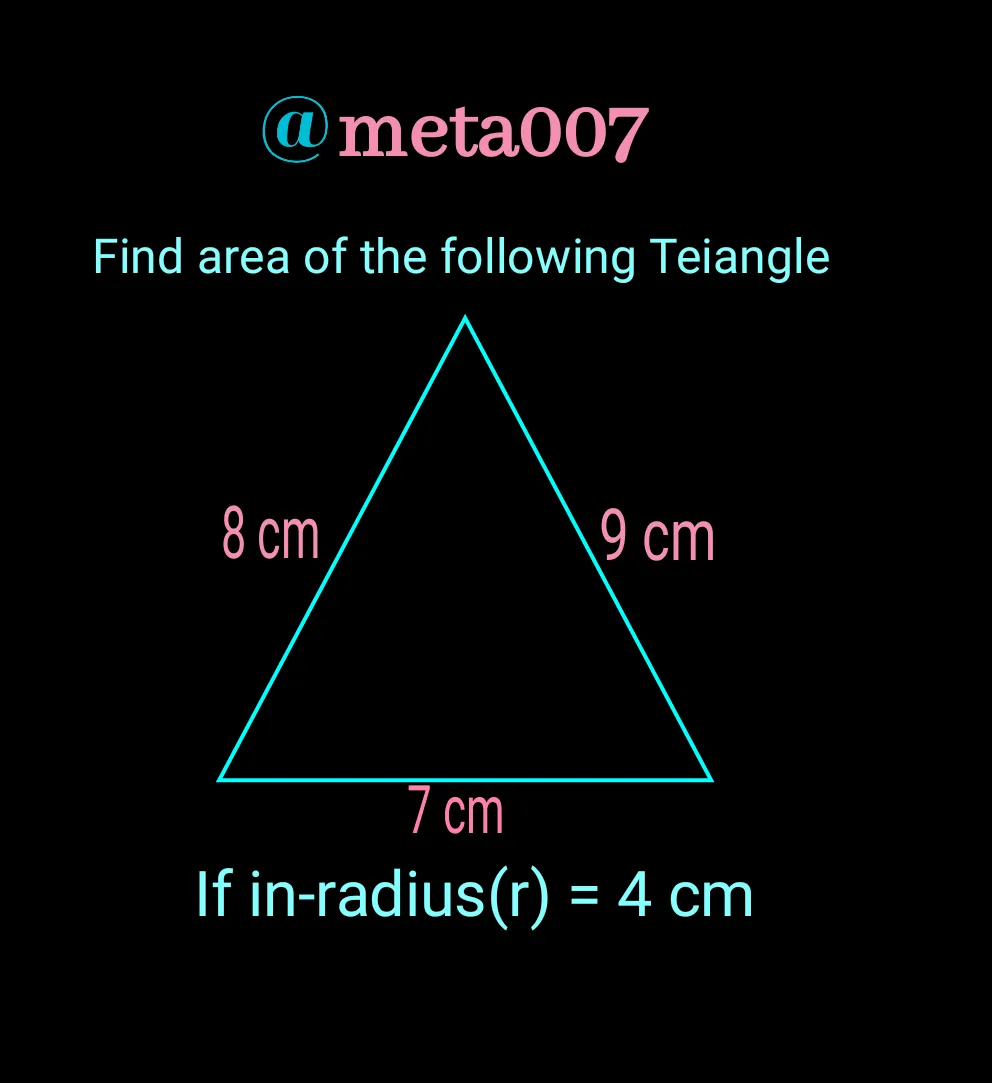
Your Options are:
- 44 square cm
- 46 square cm
- 48 square cm
- 50 square cm
My next topic will be centroid or geo-centre.
Thank you for visiting
Stay healthy
See you around
Regards: @meta007
