There are several methods to solve for the values of x, y, and z in the system of equations. Among these methods is LU Factorization Methods. One of these methods is Doolittle Factorization. Initially, represent the system of equation as a matrix of its coefficients, variables and constants.
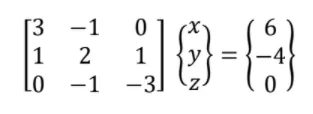
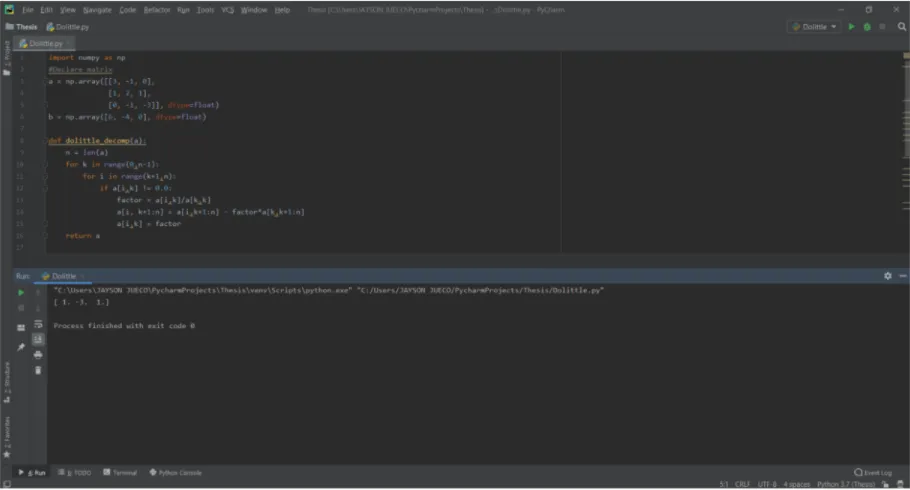
To initialize the recipe in python, we first convert the matrix representation of these equations as arrays. This can be done by declaring two set of arrays: (a) for the coefficients of the system of equations, and (b) for the constant. Each arrays are assigned as a floating point value.
a = np.array([[3, -1, 0],
[1, 2, 1],
[0, -1, -3]], dtype=float)
b = np.array([6, -4, 0], dtype=float)
The first step is to decompose the matrix using the step of Gauss elimination. Recalling Gauss elimination, the initial step is to perform forward elimination. With this, the first unknown variable in the second through the nth equations is eliminated. Start by multiplying the quotient of [col 1, row 2] and [col 1, row 1]. After its execution, subtract the result to all elements in row 2 of the matrix.
for k in range(0,n-1):
for i in range(k+1,n):
if a[i,k] != 0.0:
factor = a[i,k]/a[k,k]
a[i, k+1:n] = a[i,k+1:n] - factor*a[k,k+1:n]
a[i,k] = factor
A for loop is implemented to perform the repeated step of eliminating the second variable through the nth row. The for loop terminates when the nth row has only one non-zero element. We can implement the decomposition of the coefficient matrix as a function that returns the decomposed matrix.
def dolittle_decomp(a):
n = len(a)
for k in range(0,n-1):
for i in range(k+1,n):
if a[i,k] != 0.0:
factor = a[i,k]/a[k,k]
a[i, k+1:n] = a[i,k+1:n] - factor*a[k,k+1:n]
a[i,k] = factor
return a
To solve the values of each unknown variables, we perform both forward and back substitution for the decomposed matrix and the constant matrix. The forward substitution is configured in python using a for loop. The algorithm is implemented as:
for k in range(1,n):
b[k] = b[k] - np.dot(a[k,0:k],b[0:k])
Similar with Gauss method, we write the python recipe for back substitution as:
for k in range(n-1,-1,-1):
b[k] = (b[k] - np.dot(a[k,k+1:n],b[k+1:n]))/a[k,k]
Now, we write a function containing both the algorithms for forward and back substitution. The function would return the values of the unknown variables for the system of equations. The recipe can be written as:
def dolittle_solve(a,b):
n = len(a)
for k in range(1,n):
b[k] = b[k] - np.dot(a[k,0:k],b[0:k])
for k in range(n-1,-1,-1):
b[k] = (b[k] - np.dot(a[k,k+1:n],b[k+1:n]))/a[k,k]
return b
Hence Doolittle involves decomposing the matrix to solve for unknown variables. We can compile the recipe as:
a = np.array([[3, -1, 0],
[1, 2, 1],
[0, -1, -3]], dtype=float)
b = np.array([6, -4, 0], dtype=float)
for k in range(0,n-1):
for i in range(k+1,n):
if a[i,k] != 0.0:
factor = a[i,k]/a[k,k]
a[i, k+1:n] = a[i,k+1:n] - factor*a[k,k+1:n]
a[i,k] = factor
def dolittle_decomp(a):
n = len(a)
for k in range(0,n-1):
for i in range(k+1,n):
if a[i,k] != 0.0:
factor = a[i,k]/a[k,k]
a[i, k+1:n] = a[i,k+1:n] - factor*a[k,k+1:n]
a[i,k] = factor
return a
def dolittle_solve(a,b):
n = len(a)
for k in range(1,n):
b[k] = b[k] - np.dot(a[k,0:k],b[0:k])
for k in range(n-1,-1,-1):
b[k] = (b[k] - np.dot(a[k,k+1:n],b[k+1:n]))/a[k,k]
return b
The values of the assumed system of equation are x = 1, y = −3, and z = 1. The program result is shown below. The result is shown in the cover image.
