This is the third part on my Simulation Hypothesis series. You can find Part 1, and Part 2 here.
In this post I am going to explore the same question that eventually lead me to the conclusion that it was indeed very possible we are inside of a simulation. I will cover mostly the same information I did in that post from five years ago but it will also be influenced by my thoughts since then as well as dialogs I've had with other people.
The post from 5 years ago is here: If reality were only a simulation how would WE the simulants be able to know for sure?
DEFINITION:
I was asked today what a "simulant" was. Until I was asked I hadn't really considered that by using this word that I may or may not have made up (I first used it five years ago) that not everyone would understand what I meant by it. Before proceeding with the main thrust of this post I'll tell you what the word SIMULANT means to me.
SIMULANT: Is the things and entities within the simulation that are being simulated. The simulation itself encompasses all. The simulants are parts within that simulation. Depending upon what level you view them they can be as small as atoms, they can be the people, the animals, the plants, the simulated wind, particular rules, or groups of these things. Simulants would refer to anything inside of the simulation that is being simulated. That defines ALMOST everything inside the simulation. There are some cases where it may not apply but those are for another day and another post.
If we were inside of a simulation how could we know?
Five years ago I asked this exact question as I began thinking about it and writing about it. I knew that if we were inside of a simulation then we would be in some form of closed container (my initial concept) and thus unless the simulation was designed in a way to allow things from inside the simulation to see outside of it we would not have the mechanism of detecting such a thing.
If there are no windows to let you see out, then you can't see out.
If there are no communication devices to let you communicate outside then you can't communicate with outside of the simulation.
If there is no feedback within the simulation that is accessible by the simulation to determine how it is operating overall then you wouldn't know.
This is the initial question of mine:
If you are inside of a simulation that is a closed system and has no way to "see" outside of it how would you know you were in a simulation?
My concept of simulation has expanded since then. This will become more clear in some up coming posts. For now this particular post will treat the simulation as though it is closed. By this mechanism I can explain the thoughts that eventually convinced me it is indeed possible.
How can I find out a "How"?
To detect something we need to measure or observe something. How can someone observe something when there is no window or mechanism for observing the thing? This is especially unlikely and seemingly impossible when you consider any tool you develop is also within the same constraints. It does seem impossible.
Until you consider our own simulations. Our simulations began as simple. They have rapidly progressed over time and are becoming closer and closer to approximating a reality all of the time.

(Source: Unreal 5 Engine)
Sometimes simulations are for modeling scientific concepts, trying to predict weather (we still have trouble there), creating models to maybe explain phenomena that is too large for us to actually build and test experiments (e.g. motions of planets, solar systems, galaxies, etc.) We create simulations to test out our hypothesis about such things. Yet the planet inside of our simulation does not look back at us as it flies by on our computer screen, or in our physical Planetarium.
As I did with the original post I am going to take a journey through the evolution of our simulations. Along the way I will point out some things of interest that ultimately formed the only way I have thought of to know we are in a simulation IF it is a closed simulation with no way to see outside of it. The way we can tell from within it, by observing what we can observe.
What are some things people have observed?
The concept of intelligent design has been popular for a long time. People have been seeking evidence of that intelligence and there are some compelling discoveries. Many books and many studies have been created around them.
The Golden Ratio(1|2|3) is one such observation that has been studied and written about extensively. You can (and should) do your own research on it as it is extremely fascinating. I have shared three links here where I also pulled the following images from.

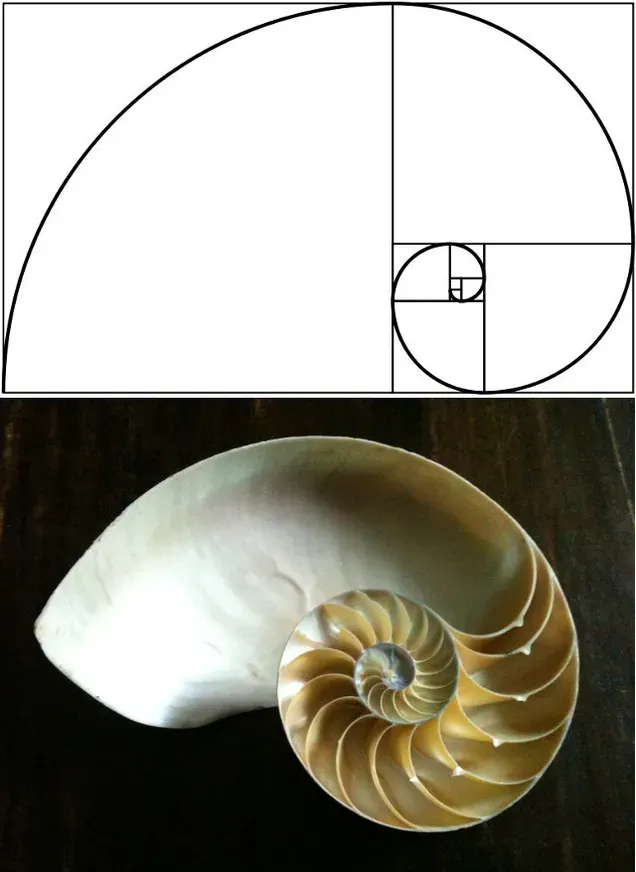
The Fibonacci Sequence(1|2|3) is another mathematical sequence that we use for creation of our own models and systems and it repeats often in nature.

Fractals(1|2) as a field of study was discovered. Of them the Mandelbrot Set (Image below) is probably the most well known. This opened the door for simulating and creating most things in nature within OUR simulations that we create.

These things are often pointed out as evidence of intelligent design. Interestingly enough they are also exactly what you might expect to see inside of a simulation that is using a term known as procedural generation. This is an important concept and will be touched upon in more detail in this post.
Bits, and Bytes
This section on bits and bytes is going to be likely a little dull and uninteresting. Understanding it is the key later on to the how...
Our computer simulations operate within a binary system. In this system the smallest unit is a bit. It is often considered simply much like an on/off, true/false, or 0/1 switch. It can have a value of 0 or 1. It has two possible states. We found out we could represent numbers by stringing these bits together. We have a unit known as a BYTE that is 8 bits. Each bit value much like the digits in money has an increasing power of 2 value. We represent them usually by their largest value. They will always be considered worth either 0 or that larger value. Thus they only have 2 states still.
BIT 1 = 1 (0 or 1)
BIT 2 = 2 (0 or 2)
BIT 3 = 4 (0 or 4)
BIT 4 = 8 (0 or 8)
BIT 5 = 16 (0 or 16)
BIT 6 = 32 (0 or 32)
BIT 7 = 64 (0 or 64)
BIT 8 = 128 (0 or 128)
As you turn those bits on you total their value to get your number. A byte therefore can store a value from 0 to 255. This means the byte has 256 possible states. 256 is actually the same value as if you had taken the above BIT progression and done BIT 9 = 256 (0 or 256). You can thus find out what the absolute possible number of states are for all the previous bits in any number of bits by taking the next power of two value that would proceed. Total States = (N+1) to the power of 2 (aka (N+1)^2).
We then proceeded to do all kinds of things with this process. We found that if we did 16 bits we could store 65536 different states. On 16 bit computers we would call this a WORD. In some programming languages a word is always 16 bits. Yet as far as computer central processing units (CPUs) are concerned a word is always the amount of bits the processor natively handles in things known as registers, accumulators, stores, etc. When we hear about 32 bit computers their word size was 32 bits. When we hear about 64 bit computers their word size is 64 bits.
This is important due to the number of states they can handle. Addresses for memory are tracked in this fashion. Let's talk about memory for a moment:
K (Kilobyte) = 1024 bytes
M (Megabyte) = 1024 Kilobytes
G (Gigabyte) = 1024 Megabytes
T (Terabyte) = 1024 Gigabytes
You likely have seen these terms and are familiar with them. I am sharing them for those that may not be and also so those of your that are familiar with them will be thinking about them.
With a 16 bit WORD an address could be 0-65535. That means you could at most have a 64K computer. Your RAM memory could not exceed 64K without some tricky additional registers and such added to the CPU. We did in fact add tricky registers and techniques to CPUs to compensate for this occasionally. They were not always the most ideal or performant way to handle things.
With a 32 bit WORD we suddenly had access to up to 4G (4 Gigabytes) of RAM. Certainly that should be the most we ever need right? Wrong. Within a short period of time this barrier became a huge issue. The introduction of 64 bit CPUs with a 64 bit word significantly increased the amount of addresses that could be referenced. Will we go beyond 64 bit in the future? It is very possible. If history is any indicator then YES.
That was a primer on bits, bytes, and memory. These things will be revisited later and I'll also introduce you to some other nifty types. Most specifically something known as a floating point number because it is immensely important to explaining the how.
Games, Games, oh you wonderful games...
In history as we know it we have created games. We create a play area and define rules that must be followed to PLAY the game. We extend this to other disciplines as well. When I was studying a variation of Pencak Silat (martial arts) they didn't say "Let's spar", "Let's fight", they would say "Let's play" when they were practicing with each other in freeform combat. Other styles I studied did not do this, but the "Play" aspect stuck with me. "We've taught you the rules, let's play".

We have chess with it's 8x8 two colored play area, and 16 pieces for each side with very specific rules. Every card game has a fixed number of cards and rules for how we interact with them.

Computer Games are when it becomes truly interesting as we explore the simulation hypothesis because a computer game is nothing more than a simulation that reacts to YOUR input. It is not closed. You are outside of it but you can take actions that send information into the simulation and it reacts. We enjoy watching/observing the reactions.
Our minds have an interesting ability to make other things into extensions of ourselves. As you drive eventually the car becomes an extension of you and you are unconsciously moving that car like you would an arm, or your legs. Your mind adapts and makes it an extension of you. This is similar to the concept of immersion. A well crafted game will enable your mind to for a time forget you are playing a game. You play. It becomes an extension of you.
Over time we demand more and more from our games. This one looks more realistic than that one, this one the computer controlled people (NPCs) in the game have a more life like routine they followed, this one the controls and how you move may be more natural and intuitive, etc. The sounds might get more realistic and 3d. We might introduce something like VR which further removes external stimuli and immerses us more fully in the game.
These are simulations. They are developing and evolving at incredibly rapid pace. They are also what revealed the possible HOW would we know... This post is partially about the journey of answering that. I am stepping through the same steps I went through myself as closely as I can recall. I think it is important. If I just jump to the end it becomes easier to simply dismiss without truly "seeing" and "understanding".
1962
Enter Spacewar!
Computer games had arrived...
1972
Pong

1977
Atari VCS

1983
Nintendo NES - There were plenty of other examples too. Mainly showing dates, and evolution of games.


1985
Amiga 1000 - Way ahead of everything else out there at the time


I am going to stop with the history of gaming here as I'll run out of space and won't be able to get to what the purpose of this post was. I will revisit games and other simulations on computers in a bit. I mainly wanted to show how rapidly they were progressing in a short amount of time. They are imaginary light years beyond that state today.
Let's get into the how would we know...
Enough already - How would we know?
When we have seen oddities in our own complex simulations they have generally been due to running into barriers in the amount of detail the numbers used in the simulation could express. This is why I bothered explaining how bits and bytes work. You should know by those things that we are limited in how much information we can represent with them.
As we discovered fractals this limitation would also limit how far we could zoom. As we create procedural worlds that are completely generated by math such as Minecraft they actually have a limit on how far you could travel before you started seeing problems.
I call this the bounds of infinity. We know what infinity is supposed to mean. Yet when we try to simulate it within computers and we restrict ourselves limited by numbers the computer handles then we restrict infinity to the bounds/limits that those bits can represent. We experienced it for example when we had the 4 gigabyte memory limit due to WORDS being only 32 bits in length.
These limitations pop up in our simulations and games if you push the boundaries of infinity. In fractals you start to lose the detail and it becomes blockier and blockier and eventually your screen would be just a single solid color. The detail in the fractal itself is still there and could be zoomed inward on infinitely. The problem is that would require more and more decimal places and eventually the number of bits you use ends and that detail becomes lost. When that detail cannot be expressed any further you cannot zoom any further.
In games like Minecraft they use mathematical functions known as noise functions which when fed specific information (coordinates, height, random seed value, etc) they can precisely recreate a procedural area. You can generate a very detailed and unique looking world with just a few numbers as input. There are limits. It too is impacted by the same thing as the fractals. If you were to travel far enough in any direction (it turns out it is quite far) strange things will begin to occur, larger blocks, groups of trees where you'd expect one, and eventually just a big block.
So as we push the boundaries of our own simulations we encounter limitations in the device we are running the simulation on AS WELL as limitations in how the games were coded. We begin to notice odd things.
Now assuming that our vast reality is running in some kind of device. Could it possibly have similar limitations? It need not be binary. Yet if it has limitations isn't it possible we might be able to tell we were in a simulation by doing the same thing that exposes our own simulations problems?
If we push outward or inward towards infinity if we were in a simulation and it was using any technique we are aware of in our own we should begin to see odd things happen. Things that seem out of place, don't look right, or suddenly differ from everything we have observed and can explain.
While simply seeing these oddities may not mean it is a simulation. They very well could. That is exactly one of the things something inside a closed simulation could intentionally seek out if they thought of it.
With that stated...
As we zoom in more and more on a microscopic level have we seen oddities?
I'd say yes. We also have the odd behavior of quantum particle/waves that seem to respond to the observer. Almost like a simulation responding to an observer and trying to procedurally generate content.
I don't know if we have gone OUTWARD far enough to have witnessed such things. Perhaps we have, because I am not at all up to date on the latest things in that area of study.
How would we know? See what happens as you explore infinity. If you find boundaries in some places that should be infinite then perhaps you are in a simulation.
Floating Point, and our simulations...
I have now shared with you the possible HOW that I came up with five years ago when I asked this question. To me the observations in Quantum mechanics, and the strange things we keep finding in Physics lead me to think it was indeed possible we were in a simulation. I even would go so far as to say I personally think it is likely we are. That is my current opinion and I certainly don't require any of you to agree. You need to make your own choices, and draw your own conclusions. I am not at all dogmatic on this. I'd say I give it a 75% chance in my mind at the moment. I just made that number up as a guess on how I think I view it.
I mentioned some things above that I'd like to now visit in a little more detail for those of you that may be interested.
Most of these simulations use a form of number in computers known as a floating point number. In the earlier examples on bits I demonstrated how numbers from 0-65535 example can be represented by 2 bytes. Those numbers were positive and they had no decimal places. For most complex math involved in fractals, simulations, and procedural generation we need the ability to handle negative numbers and we need the ability to handle decimal points.
To handle a negative number you can use a bit to represent positive or negative. Now those two bytes would represent a number from -32767 to 32767. Though as you can see it actually cut the size of the maximum positive number it could represent in half. It still doesn't have decimal points.
What if we took 5 of the remaining 15 bits and made those the decimal part of the number? That would be 10 bits for the whole number part, and 5 bits for the decimal parts. Well we'd be able to represent a decimal value from 0-31. Not particularly useful. That wouldn't even cover the decimal point in monetary conversions. Yet doesn't it seem like a waste of space to have that exist when there are no decimal places. What if the whole number was simply 1 and the rest should be decimal places, or 3 like PI. If we expressed PI we'd need 2 bits to represent the 3 but wouldn't it be nice to have the remaining bits available so we could express the decimal portion of PI as much as possible?
We come up with the idea of using some of the bits to instead represent the position of the decimal point. Because it can move around we call it a floating point.
When you hear people talk about floating point numbers they are referring to the computer representation of real numbers where the position of the decimal point floats around in terms of bits as needed.
I used 16 bits for my example here which is quite bad for floating point. Most floating point numbers in computers are 4 bytes in length today or 32 bits. There is another form of floating point often called a DOUBLE that is 8 bytes or 64 bits.
Which one the simulation was written to use makes a difference on how far that simulation can go before infinity starts to break down. There are tradeoffs though. Depending upon the CPU and architecture of the computer there can be a pretty big performance hit in terms of speed when using a DOUBLE. Though this may not be that big of a deal if our reality is a simulation. I'll touch more on that in the post about TIME.
This is a new record. Notice they refer to the record because of the infinity boundary. You can make your own math system with a vast amount of digits to generate these things but it is REALLY slow. That is okay though if you save the results as images and build a video afterwards. These things are not generated at real time.
Minecraft has addressed this by adding a hard border. People have made it. It must be there because there is insufficient space in the bits of the numbers for the procedural content to reliably create the world.
This barrier didn't always exist.
Until next time...
Yes it will be on TIME.



