Hello its me drifter1 again! Today we get into Java again. I will implement yet another Graph algorithm and this time we are talking about the Shortest Path Problem that can be solved mainly through Dijkstra and Bellman-Ford. Today, we will cover the first algorithm and sometime in the future I will also get into the second one that is more advanced. So, without further do let's get straight into it!
Shortest Path Problem:
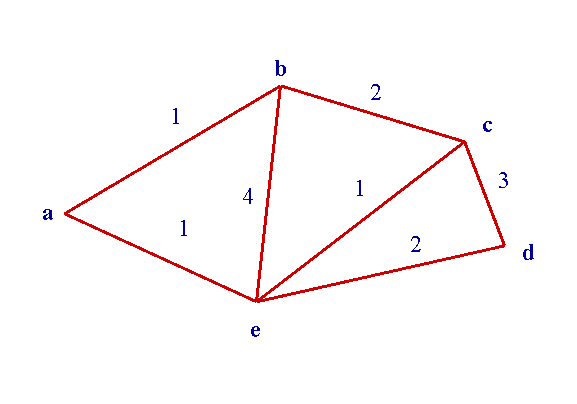
The shortest path problem is about finding the minimum distances needed to travel from a specific source vertex to all the other vertices. So, we need an algorithm that finds the minimum distances and prints them and their shortests paths out. Today I will cover one of the single-source shortest path algorithms that is Dijkstra's algorithm and later on we will also get into the Bellman-Ford Algorithm, and maybe even the Johnson's algorithm that combines the other two.
An SSSP algorithm can be useful for finding the shortest path to travel from one city (source vertex) to another. We can have weights on the edges/roads and therefore calculate the smallest weight sum or distance to travel from this first vertex/city to another one. This means that we could stop the algorithm when we found the minimum distance to a specific vertex! Single-source Shortest Path Algorithms are also used in network routing protocols that I may cover sometime in the future too :)
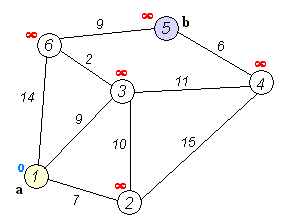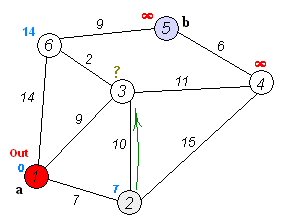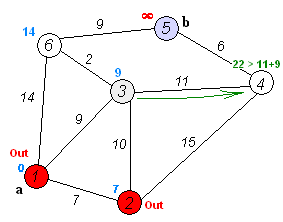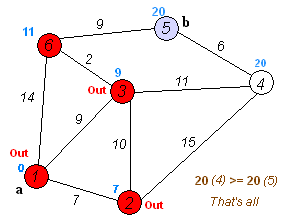
Dijkstra Algorithm Pseudocode:
The Dijkstra algorithm can be implemented using many different ways. The fastest one of these is using a minimum-priority queue with fibonacci heap implementation. This implementation is complicated and so for you to understand it better and because we already have a very good adjacency list graph implementation we will use this one instead.
For this matter I will have a minimum-priority queue inside of the algorithm code that stores vertices with distances in increasing order and keep the adjacency queue array for the neighbours of each vertex inside of the graph itself.
The pseudocode that we will implement is this one from wikipedia:
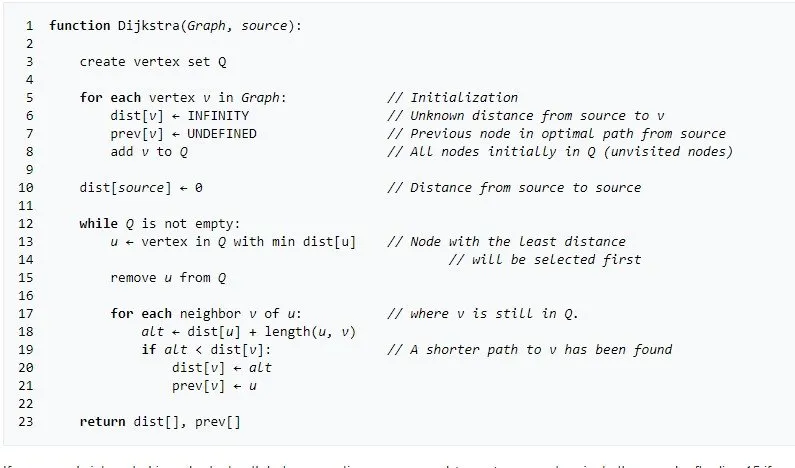
The difference is that I will not return the distances and parents, but will print the result inside of the algorithm/method itself. You will also see that some things in pseudocode sound and look simple, but get really tense when implementing it using real datastructures...
Dijkstra Implementation in Java:
We will use the adjacency List graph implementation that we used the other times as well, having a separate object/class called Edge that contains additional information like the weight of an Edge. Because, we need to store information about Vertices we will also have a object/class called Vertex that contains an id, the distance to the source vector to use in the sssp algorithm and the parent vertex. This Vertex object will not be inside of the Graph itself, but will only be used in a min-priority queue inside of our dijkstra method.
So, our classes look like this:
Edge class:

Graph class:

Vertex class:

The dijkstra method looks like this:
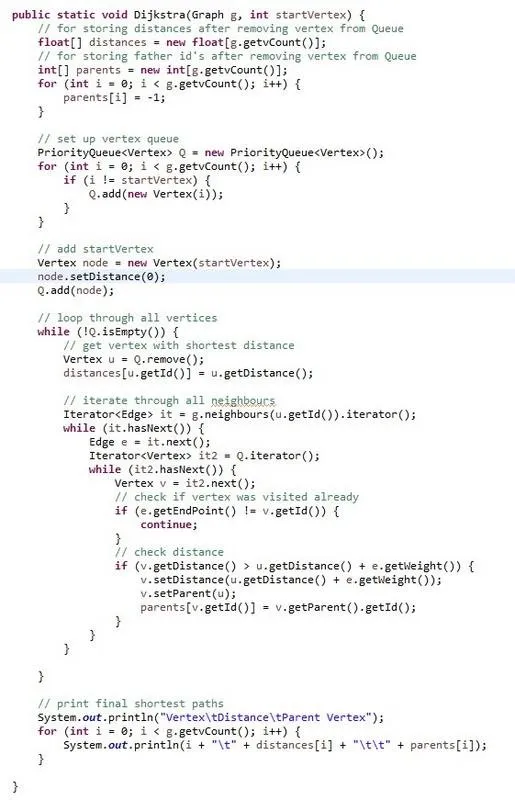
This method is a part of a TestGraphs class that looks like this:
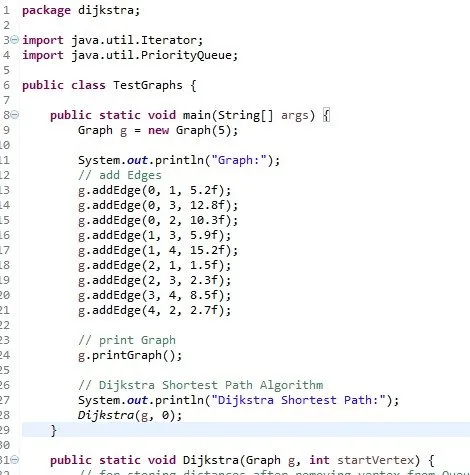
The Console prints out:
Graph:
0: 0-1 (5.2) 0-3 (12.8) 0-2 (10.3)
1: 1-3 (5.9) 1-4 (15.2)
2: 2-1 (1.5) 2-3 (2.3)
3: 3-4 (8.5)
4: 4-2 (2.7)
Dijkstra Shortest Path:
Vertex Distance Parent Vertex
0 0.0 -1
1 5.2 0
2 10.3 0
3 11.1 1
4 19.6 3
I can't take it when Steemit puts horizontal scrollsbars or starts "destroying" my Code and so I made screenshots inside of the post. But, you can get the Code in the following links of pastebin as well:
TestGraphs/Dijsktra Algorithm class
Don't forget to put them all in a package called "dijkstra" or you can also just remove the 1st line!
And this is actually it and I hope you enjoyed it!
Finally some Coding again, Mathematics is cool and useful, but nothing is better than a big Java program! As I mentioned in this post, there will be another post related to this one that will be about the Bellman-Ford Algorithm. And even more algorithms for Graph Problems are yet to come. :)
Bye!
