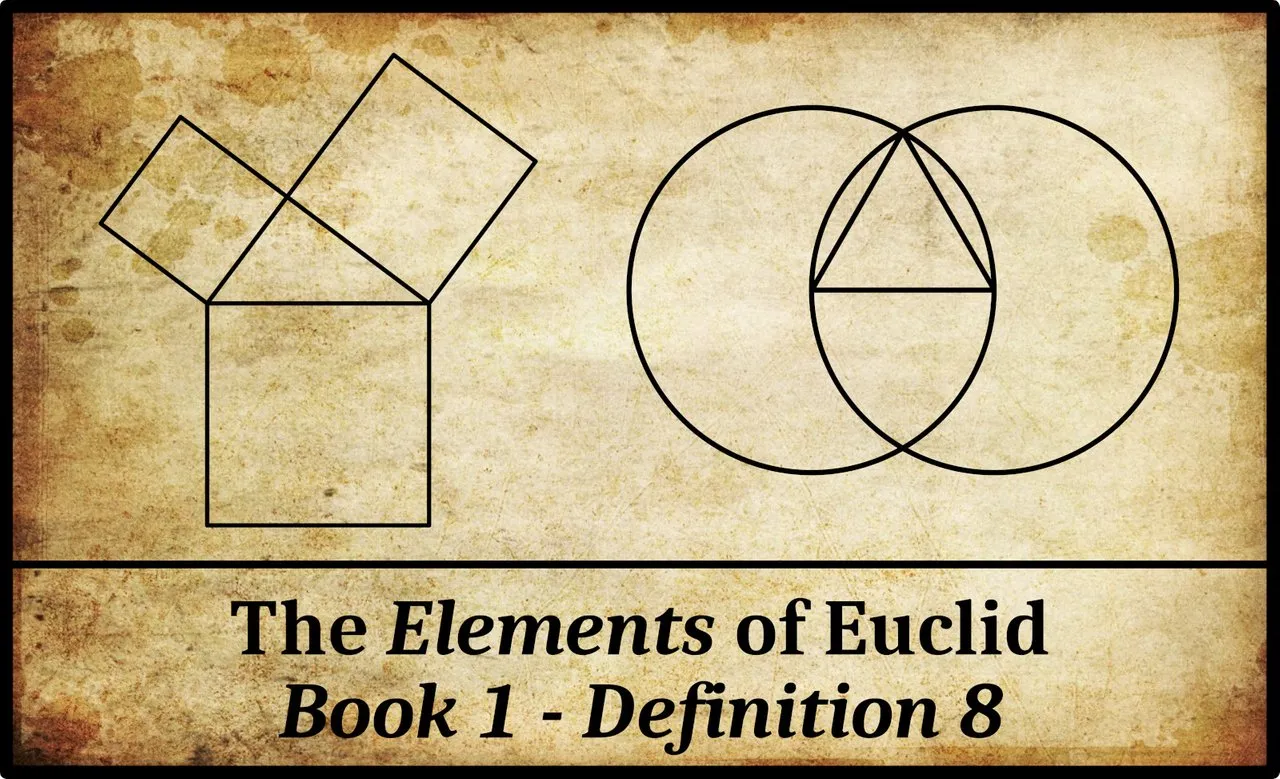
In Book 1 of Euclid’s Elements, Definition 8 reads (Fitzpatrick 6):
| Greek | English |
|---|---|
| ηʹ. ̓Επίπεδος δὲ γωνία ἐστὶν ἡ ἐν ἐπιπέδῳ δύο γραμμῶν ἁπτομένων ἀλλήλων καὶ μὴ ἐπ ̓ εὐθείας κειμένων πρὸς ἀλλήλας τῶν γραμμῶν κλίσις. | 8. And a plane angle is the inclination of the lines to one another, when two lines in a plane meet one another, and are not lying in a straight-line. |
Euclid’s concept of an angle is a difficult one to grasp. It is not quite the same as our modern idea of a plane angle:
The concept of angle is a very important concept for all of Greek geometry. Many of the propositions require angles even for their statements. The two lines are meant to emanate from the same point; two intersecting lines will actually make four angles. The concept is also a difficult one, and, surprisingly, broader than our modern concept of angle.
As can be seen from the next definition of rectilinear angle, angles do not have to have straight sides; they can have curves as sides. The size of the angle does not depend on the length of the sides, but is determined only by how the two sides meet. In the Elements nearly all the angles are rectilinear, but angles with curved sides appear in proposition III.16. In that proposition, a so-called horn angle CAE is described as the angle between a circle and a straight tangent line and is shown to be smaller than any rectilinear angle FAE. Even though the curved side of the horn angle extends beyond any rectilinear angle, it is considered to be smaller since near the vertex A of the angle, the curvilinear angle CAE is entirely contained in the rectilinear angle FAE. Thus, an angle doesn’t have an extent. (Joyce)
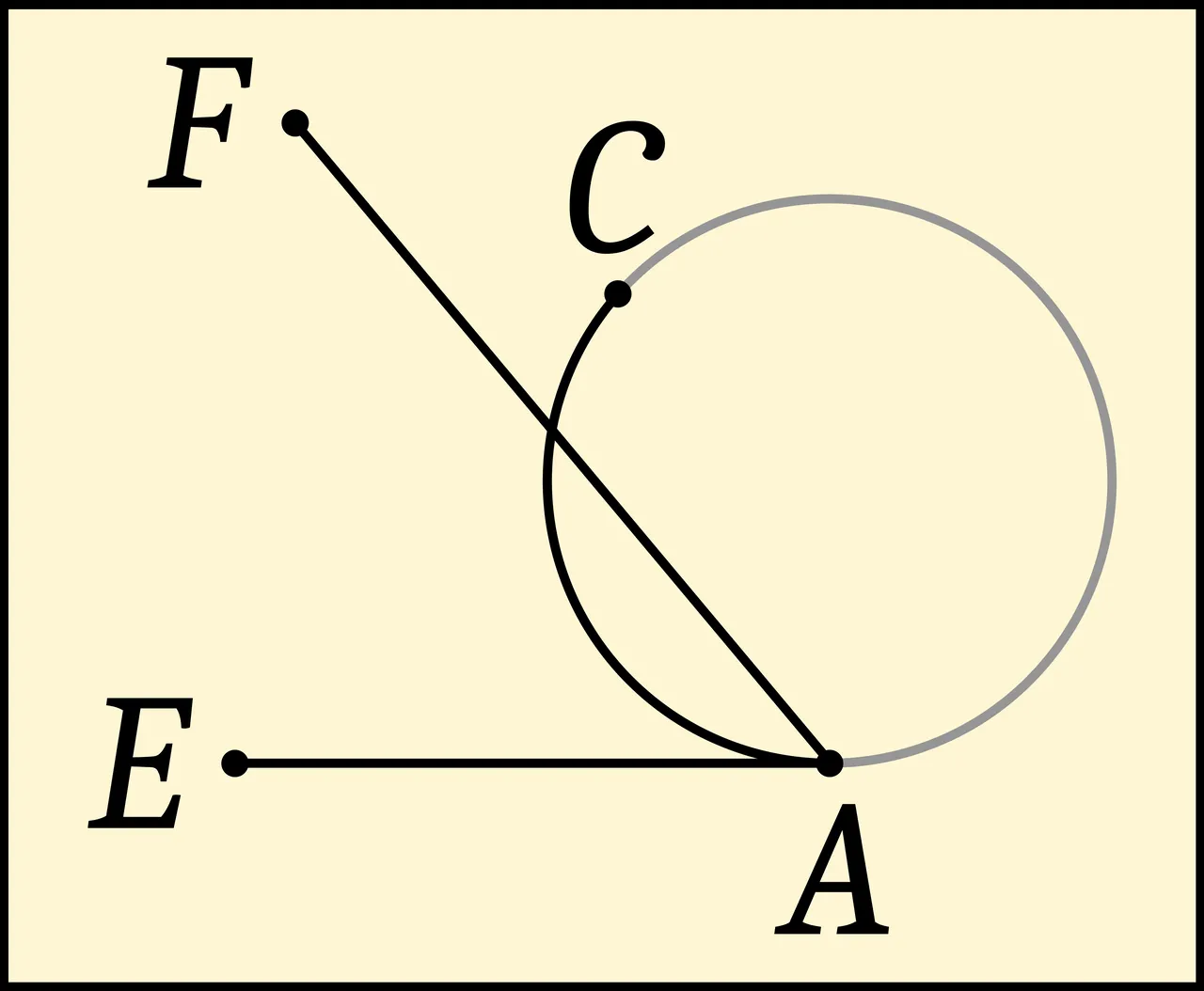
Remember that Euclid’s definition of a line includes not only straight lines, line segments and half-lines (rays), but also curves of all kinds. A Euclidean plane angle, then, can be rectilineal or curvilineal.
Euclid’s definition of a plane angle is thought to be an original idea of his own:
The phrase “not in a straight line” is strange, seeing that the definition purports to apply to angles formed by curves as well as straight lines. We should rather have expected continuous (συνεχής) with one another; and Heron takes this to be the meaning, since he at once adds an explanation as to what is meant by lines not being continuous (οὐ συνεχεῖς). It looks as though Euclid really intended to define a rectilineal angle, but on second thoughts, as a concession to the then common recognition of curvilineal angles, altered “straight lines” into “lines” and separated the definition into two.
I think all our evidence suggests that Euclid’s definition of an angle as inclination (κλίσις) was a new departure. The word does not occur in Aristotle; and we should gather from him that the idea generally associated with an angle in his time was rather deflection or breaking of lines (κλάσις). (Heath 176)
In his Commentary on the First Book of Euclid’s Elements, Proclus has a lengthy discussion of Definition 8, which testifies to the difficulty of this Euclidean concept. Like Heath, Proclus is troubled by the inclusion of the phrase “not in a straight line”, which he considers redundant with regard to certain angles (Morrow 103-104). He also notes a deficiency in Euclid’s definition:
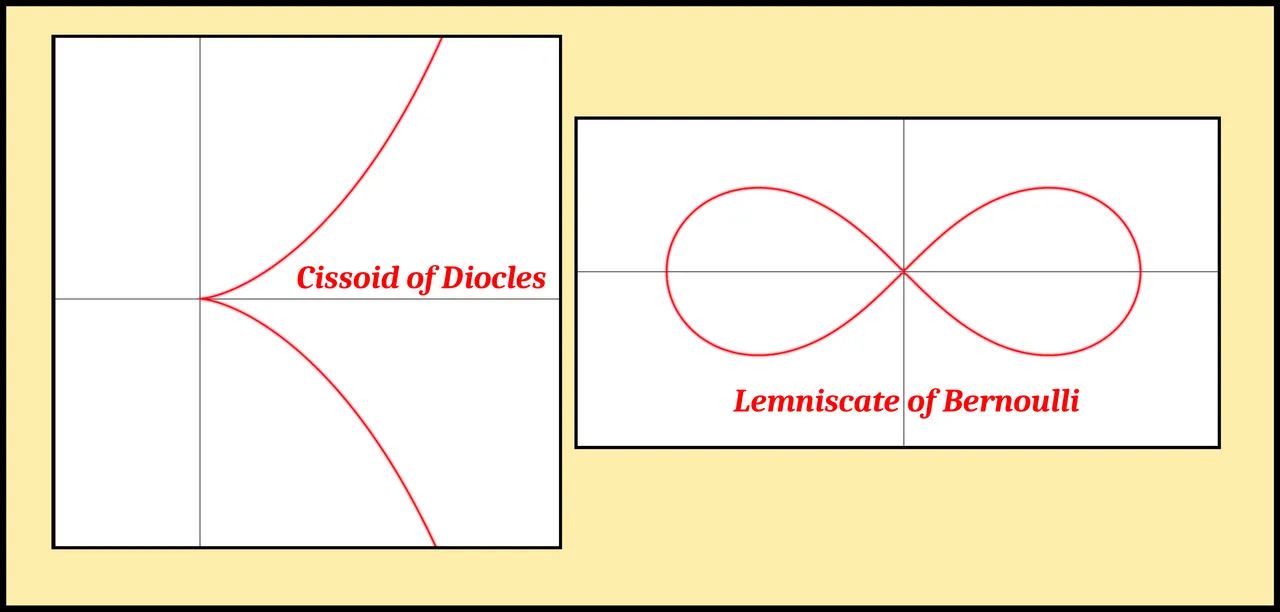
Now this definition, in the first place, seems to deny that an angle can be produced by a single line. Yet the cissoid, a single line, makes an angle, and so does the hippopede. We call “cissoid” the line as a whole, not its parts (for then we could say that it is its parts converging on one another that make the angle); likewise it is the whole spiric section, not its parts, that we call the hippopede. Thus each of them, being one, makes an angle with itself, not with another line. (Morrow 103)
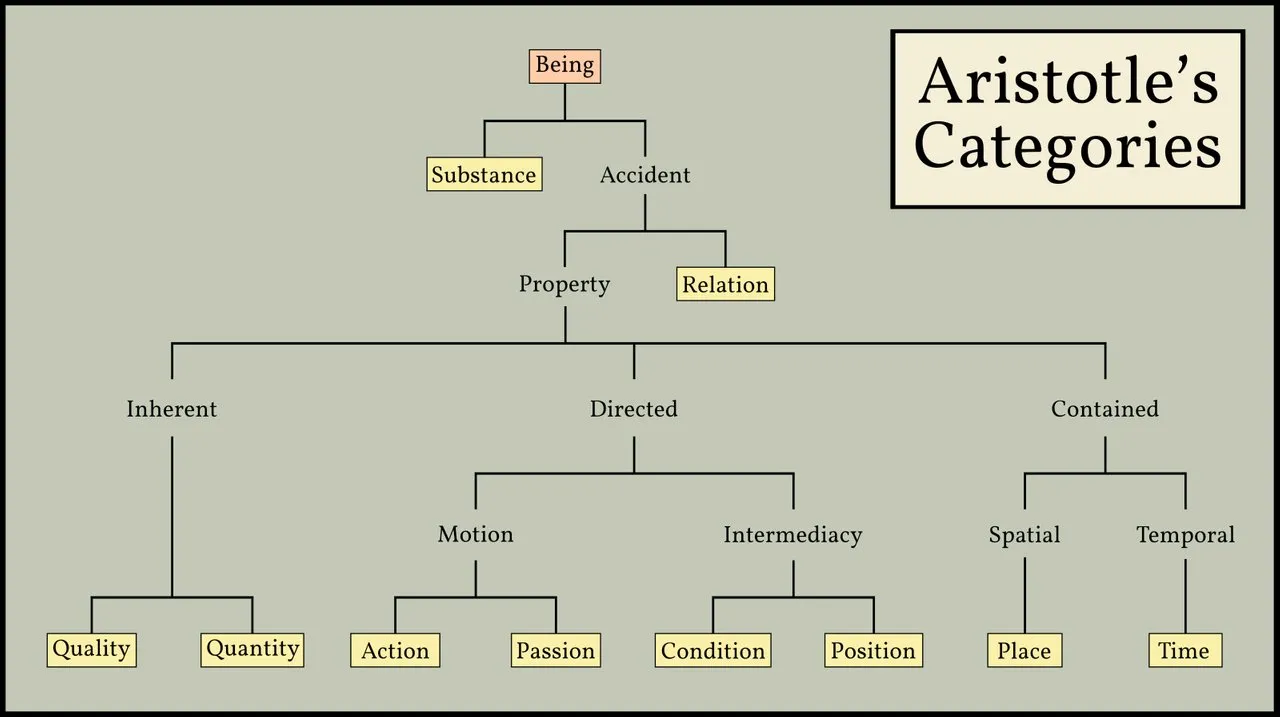
Aristotle’s Categories
The Categories is the opening volume of the Organon, a collection of six works on logic by Aristotle. In this short book, Aristotle attempts to compile an exhaustive list of the kinds of things that can be the subject or predicate of a proposition. His analysis resulted in a list of ten categories, or κατηγορίαι, as he calls them:
| English | Greek | Latin |
|---|---|---|
| substance | οὐσία | substantia |
| quantity | ποσόν | quantitas |
| quality | ποιόν | qualitas |
| relation | πρός τι | relatio |
| place | ποῦ | ubi |
| time | πότε | quando |
| position | κεῖσθαι | positio |
| condition | ἔχειν | habitus |
| action | ποιεῖν | actio |
| passion | πάσχειν | passio |
To which of these ten categories do geometric angles belong? The difficulties posed by this simple concept are reflected by the fact that mathematicians have been debating this question for centuries. In Proclus’ day—5th century CE—the question was still unresolved. An angle was variously believed to be a quantity, a quality, or a relation. Proclus, however, suggested that the truth was not so cut and dry:
Some of the ancients put the angle in the category of relation, calling it the inclination either of lines or of planes to one another; others place it under quality, saying that, like straight and curved, it is a certain character of a surface or a solid; others refer it to quantity, asserting that it is either a surface or a solid quantity ... But let us follow our “head” and say that the angle as such is none of the things mentioned but exists as a combination of all these categories, and this is why it presents a difficulty to those who are inclined to make it any one of them. (Morrow 98 ... 99-100)
This solution of the problem was apparently proposed by Syrianus, Proclus’ teacher and the second “head” of the Neoplatonic Academy at Athens. When Syrianus died in 437 CE, Proclus succeeded him as head of the school.
Proclus believed that Euclid himself thought of an angle as a relation (Morrow 101), but Heath disagrees:
Euclid and all who called an angle an inclination are held by Syrianus to have classed it as a relation (πρός τι). Yet Euclid certainty regarded angles as magnitudes [ie quantities]; this is clear both from the earliest propositions dealing specifically with angles, e.g. I.9, I.13, and also (though in another way) from his describing an angle in the very next definition and always as contained (περιεχομένη) by the two lines forming it. (Heath 178)
And that’s a good place to stop.
References
- Jonathan Barnes (editor), The Complete Works of Aristotle, Volumes 1 & 2, Princeton University Press, Princeton, NJ (1984)
- Richard Fitzpatrick (translator), Euclid’s Elements of Geometry, University of Texas at Austin, Austin, TX (2008)
- Thomas Little Heath (translator & editor), The Thirteen Books of Euclid’s Elements, Second Edition, Dover Publications, New York (1956)
- Johan Ludvig Heiberg, Heinrich Menge, Euclidis Elementa edidit et Latine interpretatus est I. L. Heiberg, Volumes 1-5, B G Teubner Verlag, Leipzig (1883-1888)
- Henry George Liddell, Robert Scott, A Greek-English Lexicon, Eighth Edition, American Book Company, New York (1901)
- Glenn R Morrow (translator), Proclus: A Commentary on the First Book of Euclid’s Elements, Princeton University Press, Princeton, NJ (1970)
Online Resources

