Warning: This post is highly technical in nature
Hi Everyone,

This post is the technical follow-up to my post ’Quality of life as quality of time’. In the above-mentioned post, I discussed valuing quality of life in the context of experiencing time. In this post, I will delve into the technical detail of the algorithms that I am applying to a model that I am developing to express utility (satisfaction) as a function of time.
Key Algorithms
The model consists of two algorithms. One algorithm models personal utility and the other models external utility. I have defined personal utility as the utility/satisfaction that a person obtains through his or her own activity. I have defined external utility as the utility obtained by those, other than ourselves, that have benefited from our activity.
The personal utility algorithm is the more complex of the two equations. The personal utility and external utility algorithms are expressed in Equations 1 and 2 respectively.
Equation 1: Personal Utility Algorithm
(((W+βw-n)(MWF)+(αw)(1/(w^MPF))t/α)aT+bT+ct)d
Equation 2: External Utility Algorithm
ew(MWEF)t+f(MFEF)T
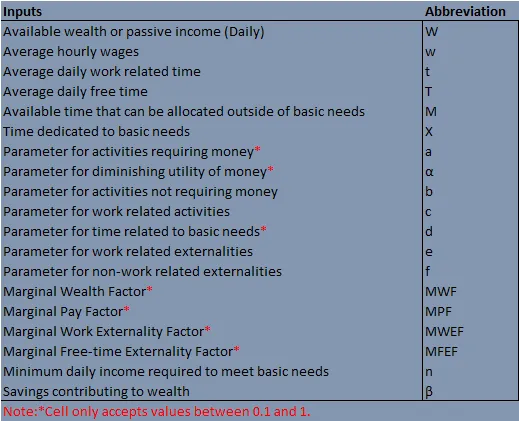
Key components of the algorithms
The algorithms can be broken into key components. The personal utility algorithm can be broken into two components. These components are utility from activities that require money and activities that require little or no money. The external utility algorithm can also be broken into two components. These components are utility obtained by external parties from paid work activities and utility obtained by external parties from non-paid activities.
Parameters in the algorithms

The algorithms contain many parameters. It is important to define each parameter and the relationships that these parameters have with each other.
Available wealth or passive income (Daily)
This parameter represents wealth or income obtained from not engaging in work. This could be interest earned, welfare payouts, or previously saved income.
Average hourly wages
This parameter represents the average net pay per hour worked. Work includes actual hours at work as well as travelling to and from work. Work related expenses should be deducted from the average hourly net pay. For example, if someone spends 8 hours at work earning $20 an hour but travels 2 hours to work at a cost of $10. Average hourly wages to be used should be $16. ‘Average hourly wages’ should be considered as real wages; i.e. does not include inflation.
Average daily work related time
This parameter represents the average amount of time involved with working. This should include travel time to work.
Average daily free time
This parameter is the average amount of time not dedicated to working or to attending basic needs such as sleeping, bathing, cleaning etc. This parameter represents the amount of time with no imposed obligations.
Available time that can be allocated outside of basic needs
This parameter is the total of ‘average daily work related time’ and ‘average daily free time’. This can also be expressed as 24 hours minus ‘time dedicated to basic needs’.
Time dedicated to basic needs
This parameter represents the time required to attend sufficiently to basic needs such as sleeping, bathing, cleaning etc.
Parameter for activities requiring money
This parameter determines the level of utility obtained directly from activities that require money. This parameter requires wealth, income and free time to produce a utility value. A higher value indicates that a person obtains a high utility from a more expensive lifestyle. This parameter has a maximum value of 1 to offset the multiplicative effect of income and wages.
Parameter for diminishing utility of money
This parameter, in part, determines diminishing value of utility obtained from money; the other parameter is the ‘marginal pay factor’. This parameter determines the extent income is subject to diminishing utility. A higher value indicates a higher portion of income is subject to diminishing utility. The inverse off this parameter is also included in the algorithm to reduce distortion to the value of utility from changing this parameter.
Parameter for activities not requiring money
This parameter determines the level of utility obtained from activities that require no or very little money. This parameter only requires free time to produce a utility value. A higher value indicates that a person can obtain a high utility from a lifestyle that requires minimal material wealth.
Parameter for work related activities
This parameter determines the level of utility obtained from activities relating to paid work. This parameter just requires time spent at work to produce a utility value. A higher value indicates that a person obtains a high level of enjoyment and satisfaction from his or her job.
Parameter for time related to basic needs
This parameter is indicative of the obtainment of basic needs as outlined below:
- Shelter
- Food
- Water
- Sanitation
- Clean Air
- Clothing
If all of the above needs are obtained, a score of one should obtained. If any of the above are not met, the value should be less than one. All parameters in the algorithm are dependent on ‘basic needs’ (multiplied across the algorithm). If ‘basic needs’ are not met, utility is greatly reduced. This approach is consistent with theory in regards to the importance of meeting daily basic needs.
Parameter for work related externalities
This parameter is included in the external utility algorithm. This parameter determines the value society obtains from work provided by a person. This parameter has a multiplicative relationship to wages and is subject to diminishing returns. The greater value a person’s work provides to society, the higher the value of the parameter. Wages is included in the algorithm as indication of wages being representative of value added.
Parameter for non-work related externalities
This parameter is included in the external utility algorithm. This parameter determines the value society obtains from a person when they are not at work. This parameter is subject to diminishing returns. The more a person contributes to society when not engaging in regular paid work, the higher the value of this parameter.
Marginal Wealth Factor
This parameter is used to determine the extent of diminishing utility obtained from income not obtained from ‘current’ work. A lower value indicates a greater diminishing effect. The value of the parameter must remain below one; a value above one would not produce a diminishing effect.
Marginal Pay Factor
This parameter is used to determine the extent of diminishing utility received from income obtained from work. This parameter is applied with ‘parameter for diminishing utility of money’ to create a more complex diminishing returns effect. The combination of these two parameters enables the modelling of a backward bending supply curve. A lower value indicates a greater diminishing effect. The value of the parameter must remain below one.
Marginal Work Externality Factor
This parameter is used to determine the extent of diminishing utility from paid work. A lower value indicates a greater diminishing effect. The value of the parameter must remain below one.
Marginal Free-time Externality Factor
This parameter is used to determine the extent of diminishing utility from activities not relating to paid work. A lower value indicates a greater diminishing effect. The value of the parameter must remain below one.
Minimum daily income required to meet basic needs
This parameter is the daily income requirement to meet basic needs. This parameter is subtracted from wealth and passive income. If wealth and passive income net of this parameter reaches zero, ‘parameter for time related to basic needs’ could be manually reduced to indicate daily basic needs cannot be met. Some societies provide directly for basic needs without the requirement of payment.
Savings contributing to wealth
This parameter represents the percentage of hourly wages that have contributed to daily available wealth. For example, if someone saves 25% of their income from working 8 hours a day at a net hourly wage of $20. This parameter should equal 2 ((8×20×0.25)/20=2).
Obtaining parameter values

For the algorithms to function, the parameters used need to be reliable and representative of people and society. There are several methods of collecting data. The two methods that I prefer involve either observing behaviour (e.g. revealed preference) or collecting data directly (e.g. stated preference surveys).
In the ‘Economic Social Utility Analysis’ model, I have constructed a basic survey containing questions that can be used to determine the importance of various determinants of each parameter. I will explain these questions and my proposed method of decoding the responses to these questions in another post, in which, I will describe how the ‘Economic Social Utility Analysis’ model functions.
Scrutiny of relationships between parameters

The stating of any relationship between parameters should be subject to scrutiny. This post only briefly covers some links between the relationships stated and theory. Before the first version of the algorithms can be considered finalised, each relationship within the algorithm needs to be supported by evidence or by established theory.
Variables vs. parameters

So far, all inputs into the algorithms have been described as parameters. Some of the parameters will be treated as variables. ‘Average daily work related time’ or ‘average daily free time’ will be treated as variables that people are able to influence. Some of the other parameters can become variables under certain circumstances.
Absence of diminishing returns to time

For the algorithms, I have adopted diminishing returns to income and wealth but not time. This approach has been proposed for two reasons.
Time is finite in nature. Everyone gets just 24 hours a day and a less clearly defined but still finite number of years to live. The number and range of activities that a person can engage in across a lifetime should strongly limit the extent of any diminishing returns to time.
Including a diminishing return in the equation would also complicate the algorithm in regards to adopting usage of time as a variable. To determine an optimal time for work and non-work activities requires the differentiation of the personal utility algorithm in respect to time.
Conclusion

In this post, I have described the algorithms that I developed for my ‘Economic Social Utility Analysis’ model; these algorithms are still a work-in-progress and will undergo further testing.
I have developed an Excel-based model that will be used to initially test the algorithms and eventually be used to apply the algorithm to real world circumstances and representations of the real world.
Post Beneficiaries
The beneficiaries of this post based on the top three upvotes of the previous post are:
In addition to these three accounts, @doughtaker has been added as a beneficiary based on comments provided. Each beneficiary will receive 20% of the post payout. Thanks for your support.
To learn more about post beneficiaries you can read my post using the following link.






