Physics - Electromagnetism - Standing Electromagnetic waves

Custom Thumbnail that contains:

Introduction

Hello it's a me again Drifter Programming! Today we continue with Electromagnetism to get into Standing Electromagnetic waves, which are of great theoretical interest! So, without further do, let's get started!

Standing waves in general

Standing or stationary waves are the combination of two waves that move in opposite direction, but have the same amplitude and frequency. This phenomenon is the result of their interference. When waves are superimposed, their energies are either added together or cancelled out. When two or more waves are moving in the same direction, their interference produces a travelling wave. When two oppositely moving waves interact which each other, this interference produces an ocillating wave that is fixed in space. This oscillating wave follows a so called standing wave pattern, which is a vibrational pattern created within a medium when the waves that get reflected from one end of the medium to interfere with incident waves from their source. This interference makes the interference points to appear standing still. Such waves are only created at specific frequencies of vibration that we call harmonic frequencies or harmonics. At other frequencies the interference of reflected and incident waves will lead to a disturbance in the medium that is irregular and non-repeating.

The timing between the two waves is very important, cause it needs to be perfect! As we already told in my Introduction article of this "chapter" the high and low amplitude points of a wave are called crests and troughts respectively. To have a "perfect harmony" the added amplitude of these two waves must be zero, which means that their interference must be "destructive". To understand this better we introduce the so called nodes and antinodes. A node (labelled as N) is a point where no displacement is being produced by neither of the waves, which means that the amplitude at this point is zero. A anti-node (labelled AN) is a point where the amplitude goes from the maximum positive to the maximum negative displacement, vibrating back and forth between those points.

To achieve the perfect timing, we have to introduce a crest at the instant where another crest is either at the halfway point or at the end of the medium (where it will be reflected). When the other crest get's reflected the "newly" introduced crest interference with this reflected wave will always create a node in the middle of the medium. The number of nodes depends on the number of crests that were present between the two "timed" crests. To achieve an anti-node we introduce the "new" crest at the instant where another crest is at the halfway point across the medium, which will will cause a constructive interference that will create a point of maximum "added" displacement. You can clearly see that such waves can be formed under a variety of conditions!

From all this you can understand that standing waves are not actual waves, but a wave pattern that is caused by the interference phenomenon between two or more waves. It's the result of perfectly timed interference between two waves that are passing through the same medium. A standing wave is a pattern that resulting of the presence of two or more waves of the same exact frequency that travel in different directions.

Such waves are present in:

non-digital musical instruments - the vibrations or waves that we put on the instrument cover a spread of frequencies resulting into sound/music
speech - when speaking our vocal cords vibrate within a small range of frequeny.
atoms - the orbital vibration of bounded electrons around atoms (orbital region)
mathematics - harmonic sequencies are also standing waves

Standing Electromagnetic waves

Now that we covered what Standing waves are, how we achieve them and where they are present, let's talk about the theoretical concept of Standing Electromagnetic waves. What we want to try understand is if there is a way to create electromagnetic waves that don't travel/propagate through space and time, but just oscillate at a fixed point in space. First of all, as we saw last time in "EM waves in matter", Electromagnetic waves of course interact with matter, which means that they can be reflected by the surface of a conductor or dielectric that can serve as a reflector. From the superposition principle, that holds for electric and magnetic fields and so electromagnetic waves also, we understand that the incident and reflected wave can of course form a standing wave.

Let's suppose:

a sheet of a perfect conductor of zero resistivity in the yz-plane
a linearly polarized electromagnetic wave travelling in the x direction, striking the plane

The wave can't have a electric field component parallel to the surface, which means that E must be zero everywhere in (or on top of) the yz-plane. The indident wave induces current on the surface of the conductor, giving rise to additional electric fields, which means that the incident wave's electric field is not zero at all times in the yz-plane. The net electric field, which is the vector sum of the two fields, is zero everywhere (inside and on the surface of the conductor).

As we know, the wave equation of the source wave is:

The induced currents of course produce a reflected wave that travels in the -x direction, but has the same frequency and amplitude as the source wave, which means that this wave is described as:

The addition of those waves gives us:

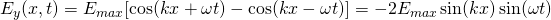
From this we see that the magnitude of the electric field is zero at:

which are the Nodes or nodal planes.

In the same notion the "total" magnetic field can be described as:

Giving us that following nodes:

All together the nodes and antinodes of the electric and magnetic field can be described by the following more general equations:

We see that the nodes of E coincide with the antinodes of B, and conversly.

We can already see that the magnetic and electric field of the electromagnetic wave are no longer in-phase like they used to be! More specifically they are out-of-phase by 90 degrees or one-fourth of a period.

Let's insert a second conducting plane, parallel to the first one and at a distance L along the positive x axis. Both conducting planes must be nodal planes for E, which means that the second plane is placed at one of the positions where E(x, t) = 0.

This shows us that a standing wave only exists when:

The wavelengths and frequencies that satisfy this condition are:

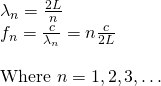
Each standing wave that gets "created" has a characteristic frequency, wave shape and node pattern!

Lastly, let's also talk about the time dependence. The Electric field is zero at all the points where "sinωt = 0", which means that:

This same equation also applies for the maximum condition of the magnetic field (the same way as with 'x'), which again shows us that the electic and magnetic fields in standing waves are out-of-phase by 90 degrees, instead of being in-phase as they are when traveling in space and time!

To understand everything visually here a "small" video that shows us how Standing Electromagnetic waves look like:

REFERENCES:

Mathematical equations that I had in this post where drawn using quicklatex!

Previous articles of the Electromagnetism series

Here we only have the previous two "chapters" and the current one!

Mutual and Self Induction:

Mutual Inductance -> Mutual Inductance, applications

Self Induction -> Self Induction, Lenz's law, Inductance of a Coil

Magnetic Energy Density -> Energy stored in a magnetic field (or inductor), Magnetic energy density, Coaxial Cable Inductance Example

R-L circuits -> R-L circuit energizing, de-energizing, Characteristic time constant

L-C circuits -> L-C circuit, oscillations, energy cases, applications

R-L-C circuits -> R-L-C circuit, oscillation, applications

Mutual and Self Induction exercises -> examples all around Mutual and Self Induction

Alternating current:

Getting into Alternating current -> Phasor diagrams, Alternating current, Average (RMS) current and voltage, Differences, Advantages/Disadvantages

Electric Reactance in AC circuits -> Resistors, Inductor and Capacitor Reactance in AC circuits

Series R-L-C circuits Impedance -> Series R-L-C circuits, Phasor Diagrams, Impedance

Power in AC circuits -> DC Resistive circuit, Power in AC circuits (resistive, reactive), Power Factor

Resonance in Series R-L-C circuits -> Series R-L-C circuit, Series Resonance

Resonance in Parallel R-L-C circuits -> Parallel R-L-C circuit, Parallel Resonance

AC Transformers -> How they work, Configurations, Types, Voltage and Current Transformer

Alternating current exercises -> examples all around Alternating current

Electromagnetic waves:

Electromagnetic Wave Introduction -> Electromagnetic waves, velocity, wave equation

Sine waves and EM wave energy -> Sine waves, energy density, EM wave power, Poynting vector, Radiation pressure / Energy momentum

Electromagnetic waves in matter -> Propagation, Angular distribution, polarization and scattering, Interaction with Conductors, Plasma and Dielectrics

Final words | Next time

And this is actually it for today's post and I hope that you enjoyed this theoretical topic! Next time we will talk about the Electromagnetic Spectrum!

Keep on drifting!