[Image 1]
Introduction
Hey it's a me again @drifter1! Today we continue with the Physics branch "Classical Mechanics" to talk about Potential and Mechanical Energy. This whole topic will be covered in 2 or 3 parts/articles, cause there are lots of things to talk about!
More specifcally, today's topics are:
- Potential Energy (in general)
- Gravitational Potential Energy
- Elastic Potential Energy
- Conservation of Mechanical Energy
- Problem Solving Strategy & Tips
So, without further ado, let's get straight into them!
Potential Energy (in general)
So, what exactly is Potential Energy? The stored potential energy of a system is a property of the entire system and not of an individual body or particle. It depends on the relative position of various parts of a system. Such energy arises in systems where the parts exert forces on each other, with magnitudes that depend on the configuration of the parts. The potential energy of a system of bodies/particles depends only on their initial and final configurations and is independent of the path the particles travel (remember conservative forces?). The commonly used notation for Potential Energy is the letter 'U'.There are various forms of potential energy including:
- Gravitational Potential Energy, which is caused by the Earth's gravity
- Electric Potential Energy, which is caused by the electric fields and Coulomb forces between charged particles (covered in the Electromagnetism series)
- Elastic Potential Energy, which is strongly connected to the elastic force
- Chemical Potential Energy, which has to do with the molecular or atomic configuration of chemcial substances
- Thermal Potential Energy, which has to do with the change in temperature of an object
Gravitational Potential Energy

[Image 2]
As we already mentioned earlier, gravitational potential energy is caused by the force of gravity. This potential energy represents the potential of doing work as result of being located at particular position in a gravitational field (like the Earth's). Considering an object of mass m, that is lifted to a height h against the force of gravity, and noting the magnitude of gravitational acceleration as g, the Work done for the object to move to that vertical distance h is exactly what we call Gravitational Potential energy.
As an mathematical equation this looks as following:
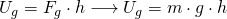
You might have noticed that we apply Newton's second law to calculate the needed force, where mg is of course the gravitational force (Fg). Also, see how we use 'Ug' to refer to gravitational potential energy, just to have an easier way of distinguishing the form/type. Removing the Force that keeps the object from falling, the objects will of course start falling back down to the ground converting it's potential energy into kinetic energy.
Something interesting about the gravitational potential energy (and potential energy as a whole) is that the 'zero' magnitude can be chosen arbitratily, meaning that we are free to choose any vertical level as the location where h = 0. The convenient zero point is mostly the ground or floor. Taking a reference point below the zero point we would end up with negative gravitational potential energy. This is something that doesn't present a problem, cause we just have to make sure that we are using the same zero point for all of our calculations.
Being at very large distances we can no longer assume a uniform gravitational field, meaning that we then have to use Newton's law of gravitation, which gives us the attractive force between two masses m1 and m2, decreasing by the distance r squared and being multiplied by the gravitational constant G. In such cases the potential energy, as a function of r, is:
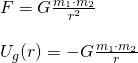
To sum up let's get into the most important points:
- The more mass an object has, the more energy it stores (U = mgh)
- The higher the object, the more energy it stores (U = mgh)
- A stronger gravitational pull (g) , results into more gravitational potential energy (U = mgh)
Elastic Potential Energy
Elastic potential energy is the energy that is stored as a result of applying a force to deform an elastic object. This energy is stored until the force is removed, making the object "spring back" to it's original shape, doing work in the process. The deformation can involve compression, stretch or twist. Objects that are designed to store such energy are:- Coil spring of a wind-up clock
- String of a Bow, which stretches
- Diving Board, when it's bent
- Rubber bands, which twist
- Bouncy balls, at the moment they are compressed
Using Hooke's law and Elasticity, Elastic Potential is given by the following Mathematical Equation:

where:
- k is the elastic (or spring) constant
- Δx the linear length a spring has been compressed or expanded by
We also define something called Plasticity, which means how likely an object is to stay stretched, when being stretched. It's the exact opposite of Elasticity, meaning that during plastic deformation energy is always being lost. This tellsus that Plastic deformation is similar to friction. So, in the end, the Elastic potential energy is what comes back out of the deformation and is the energy that was not lost as heat (increase in temperature).
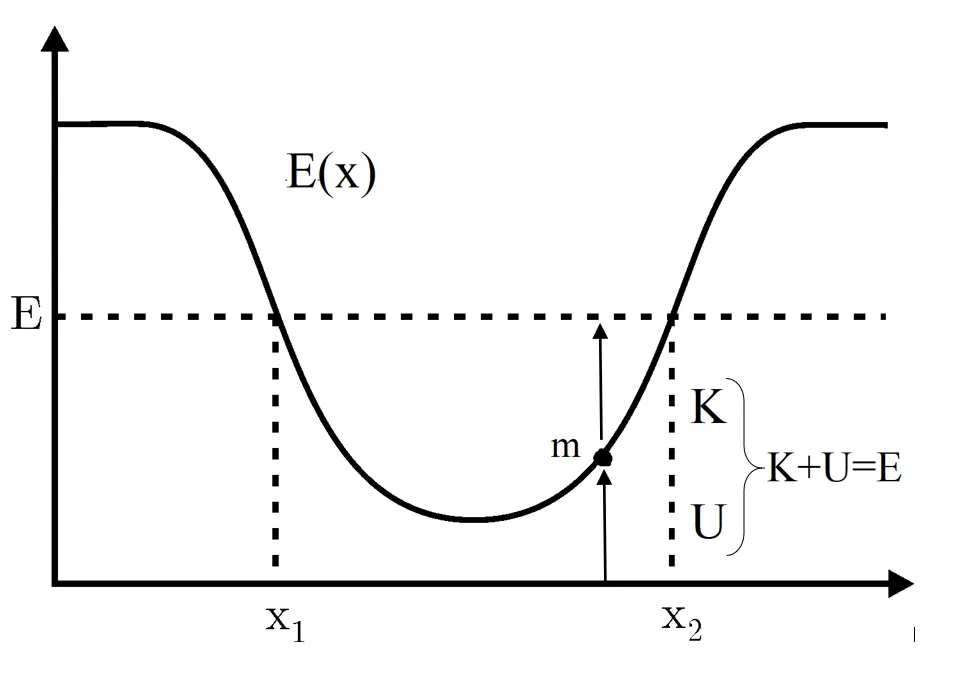
Conservation of Mechanical Energy

[Image 3]
The stored potential energy of a system can be converted into kinetic energy, by keeping the total sum of energy (kinetic energy + potential energy) constant. This sum is what we call "Mechanical Energy" of a system. But, such systems are idealized and difficult to exist in nature, cause there is always some non-conservative force like friction or air resistance that causes energy loss, lowering the mechanical energy of the system. So, Mechanical energy is the energy that is possessed by an object due to it's motion and due to it's position, together. Only objects with mechanical energy are able of doing work, meaning that mechanical energy is the ability of doing work. Any object that has the energy stored in form of kinetic or potential energy (which combined define mechanical energy) is able of doing work. Mechanical energy is what enables an object apply force to another object in order to cause it to be displaced.
The mathematical equation which describes mechanical energy is:

This was clearly an "abstract" way of defining it! Using the potential energy forms that we discussed earlier we can say that:

Of course components of this equation can be left out, if they don't apply to a specific problem! For example not all problems contain elastic objects, which add elastic PE.
Talking about problems that involve/use the conservation of energy, we can derive the law of "Conservation of Mechanical Energy", which tells us that the total amount of ME, in a closed system and in absence of dissipative (non-conservative) forces, remains constant. We already know that the path taken by an object can be ignored, which means that only the initial and final "state" of the system is needed. The only important quantities are the velocity (which gives us the kinetic energy) and height above the reference point (which gives us the gravitational potential energy).
This conservation can be written as an mathematical equation as following:
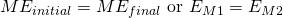
It's up to you, which notation you prefer!
Problem Solving Strategy & Tips
To solve problems around the Conservation of Mechanical Energy you should be following the steps:- Determine the system and identify the given information and quantities to be calculated.
- Examine all the forces involved in the system and determine if you know(maybe it's given) the potential energy from work done by the forces
- If you know the potential energies for the forces and all are conservative, you can apply conservation of energy in terms of PE and KE as following:
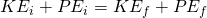
- If you know the potential energy for some of the forces, some of them are non-conservative and there are other energies that cannot be treated in terms of force and work, then you have to use the work done by the non-conservative forces and use the more general form:

- If you identified the types of work and energy involved, then you can try solving for the unknown, eliminating terms whereever it's possible to simplify the calculations. For example, we mostly choose h = 0 at either the initial or final point, so that PEg is zero at that point.
- In the end always check if your answer is reasonable by re-examining the forms of work and energy, to see if you have set up the equations in a correct way. Such things can include that the work done against friction should be negative, that the potential energy at the bottom of a hill should be less than that at the top, etc.
RESOURCES:
References
- https://www.britannica.com/science/potential-energy
- https://www.britannica.com/science/mechanical-energy
- https://www.sciencedaily.com/terms/potential_energy.htm
- https://www.khanacademy.org/science/physics/work-and-energy/work-and-energy-tutorial/a/what-is-gravitational-potential-energy
- https://www.khanacademy.org/science/physics/work-and-energy/hookes-law/a/what-is-elastic-potential-energy
- https://energyeducation.ca/encyclopedia/Gravitational_potential_energy
- https://energyeducation.ca/encyclopedia/Elastic_potential_energy
- https://www.physicsclassroom.com/class/energy/Lesson-1/Potential-Energy
- https://www.physicsclassroom.com/class/energy/Lesson-1/Mechanical-Energy
- https://www.siyavula.com/read/science/grade-10/mechanical-energy/22-mechanical-energy-05
- https://opentextbc.ca/physicstestbook2/chapter/conservation-of-energy/
Images
Mathematical equations used in this article, where made using quicklatex.
Previous articles of the series
Rectlinear motion
- Velocity and acceleration in a rectlinear motion -> velocity, accelaration and averages of those
- Rectlinear motion with constant accelaration and free falling -> const accelaration motion and free fall
- Rectlinear motion with variable acceleration and velocity relativity -> integrations to calculate pos and velocity, relative velocity
- Rectlinear motion exercises -> examples and tasks in rectlinear motion
Plane motion
- Position, velocity and acceleration vectors in a plane motion -> position, velocity and accelaration in plane motion
- Projectile motion as a plane motion -> missile/bullet motion as a plane motion
- Smooth Circular motion -> smooth circular motion theory
- Plane motion exercises -> examples and tasks in plane motions
Newton's laws and Applications
- Force and Newton's first law -> force, 1st law
- Mass and Newton's second law -> mass, 2nd law
- Newton's 3rd law and mass vs weight -> mass vs weight, 3rd law, friction
- Applying Newton's Laws -> free-body diagram, point equilibrium and 2nd law applications
- Contact forces and friction -> contact force, friction
- Dynamics of Circular motion -> circular motion dynamics, applications
- Object equilibrium and 2nd law application examples -> examples of object equilibrium and 2nd law applications
- Contact force and friction examples -> exercises in force and friction
- Circular dynamic and vertical circle motion examples -> exercises in circular dynamics
- Advanced Newton law examples -> advanced (more difficult) exercises
Work and Energy
- Work and Kinetic Energy -> Definition of Work, Work by a constant and variable Force, Work and Kinetic Energy, Power, Exercises
- Conservative and Non-Conservative Forces -> Conservation of Energy, Conservative and Non-Conservative Forces and Fields, Calculations and Exercises
You can find most of my previous articles organized per category, per series, per chapter, per article, in my recap of Summer 2018!
Final words | Next up
This is actually it for today's post! Next time we will continue with more stuff around Potential Energy.
See ya!


Keep on drifting!



