
[Image 1]
Introduction
Hey it's a me again @drifter1! After a big pause, today we finally continue with Physics and more specifically the branch "Classical Mechanics" to talk about Force and Potential Energy.
More specifcally, today's topics are:
- Force as the Potential Energy Derivative (one-dimension)
- Force as the Potential Energy Gradient (three-dimensions)
So, without further ado, let's get straight into them!
Force as the Potential Energy Derivative (one-dimension)
Thinking about the two types of conservative forces and energies that we talked about previously (elastic and gravitational) you might have noticed something!The gravity force is given by:

whilst the gravitational potential energy is given by:

In the same way, based on Hooke's law the elastic force is given by:

whilst the corresponding potential energy is:

Knowing some Mathematical Analysis, you can clearly see that the force can be found using a Differentiation on the potential energy equation. Having both the force and the potential energy in the same dimension and remembering that the work of a force is equal to the negative of the change in potential energy (W = -ΔU), we can easily talk about infinitesimal changes in position (dx).
So, in the end the force in one dimension is given by:
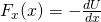
Example:
The electric potential energy of a specific system is given by:
Calculating the electric force is pretty simple and looks like this:

Force as the Potential Energy Gradient (three-dimensions)
Expanding our analysis into 2, 3 or even more dimension is quite easy! The force along the other dimensions (y and z) can be found using a differentiation on the equation using the variable of that dimension(dy and dz). This clearly gets us into partial differentiation, which is based on exactly that. So, the 3 equations for F look like this: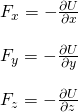
Using the unit vectors for each dimension (i, j and k) we can write:

In the end, the force is equal to the negative gradient of the potential energy:

Example:
Consider the following Potential energy equation:
Let's calculate the applied force equation in vector form!
Using partial differentiation we calculate the equation for each of the two axes:

So, the total force is:

RESOURCES:
References
- https://phys.libretexts.org/Courses/University_of_California_Davis/UCD%3A_Physics_7A/2%3A_Applying_Models_to_Mechanical_Phenomena/2.5%3A_Force_and_Potential_Energy
- http://hyperphysics.phy-astr.gsu.edu/hbase/pegrav.html
Images
- https://phys.libretexts.org/Courses/University_of_California_Davis/UCD%3A_Physics_7A/2%3A_Applying_Models_to_Mechanical_Phenomena/2.5%3A_Force_and_Potential_Energy
Mathematical equations used in this article, where made using quicklatex.
Previous articles of the series
Rectlinear motion
- Velocity and acceleration in a rectlinear motion -> velocity, accelaration and averages of those
- Rectlinear motion with constant accelaration and free falling -> const accelaration motion and free fall
- Rectlinear motion with variable acceleration and velocity relativity -> integrations to calculate pos and velocity, relative velocity
- Rectlinear motion exercises -> examples and tasks in rectlinear motion
Plane motion
- Position, velocity and acceleration vectors in a plane motion -> position, velocity and accelaration in plane motion
- Projectile motion as a plane motion -> missile/bullet motion as a plane motion
- Smooth Circular motion -> smooth circular motion theory
- Plane motion exercises -> examples and tasks in plane motions
Newton's laws and Applications
- Force and Newton's first law -> force, 1st law
- Mass and Newton's second law -> mass, 2nd law
- Newton's 3rd law and mass vs weight -> mass vs weight, 3rd law, friction
- Applying Newton's Laws -> free-body diagram, point equilibrium and 2nd law applications
- Contact forces and friction -> contact force, friction
- Dynamics of Circular motion -> circular motion dynamics, applications
- Object equilibrium and 2nd law application examples -> examples of object equilibrium and 2nd law applications
- Contact force and friction examples -> exercises in force and friction
- Circular dynamic and vertical circle motion examples -> exercises in circular dynamics
- Advanced Newton law examples -> advanced (more difficult) exercises
Work and Energy
- Work and Kinetic Energy -> Definition of Work, Work by a constant and variable Force, Work and Kinetic Energy, Power, Exercises
- Conservative and Non-Conservative Forces -> Conservation of Energy, Conservative and Non-Conservative Forces and Fields, Calculations and Exercises
- Potential and Mechanical Energy -> Gravitational and Elastic Potential Energy, Conservation of Mechanical Energy, Problem Solving Strategy & Tips
Final words | Next up
This is actually it for today's post! Next time we will continue with even more stuff around Potential Energy.
See ya!


Keep on drifting!
